Einführung
Partielle Ableitung
Um die Funktion \(z=f(x, y) = 2x^2 + 5 y\) abzuleiten, kann nach \(x\) und \(y\) separat abgeleitet werden: $$ \begin{align} \text{nach }x: \frac{\partial f}{\partial x} &= 4x + 0 \ \text{nach }y: \frac{\partial f}{\partial y} &= 0 + 5 \ \end{align} $$ Diese Ableitung kann folgendermassen visualisiert werden:
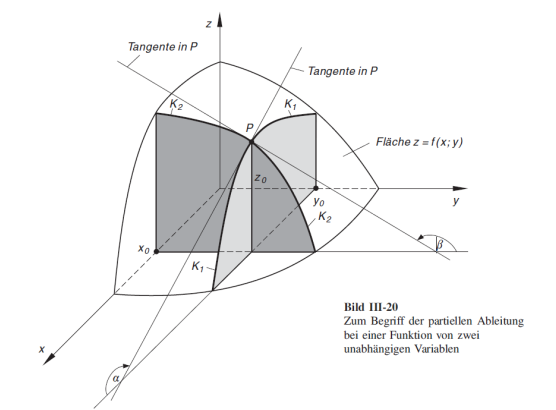
Jacobi-Matrix
Für die Funktion \(f: \mathbb R^n \to \mathbb R^m\) mit \(\vec y = f(\vec x)=\begin{pmatrix}y_1=f_1(\vec x) \\ y_2 = f_2(\vec x)\\ ... \\ y_m=f_m(\vec x)\end{pmatrix}\) und \(\vec x = (x_1, x_2, ..., x_n)^T\) ist die Jacobi-Matrix das folgende: $$ Df(x)=\begin{pmatrix} \frac{\partial f_1}{\partial x_1}(\vec x) & \frac{\partial f_1}{\partial x_2}(\vec x) & ... & \frac{\partial f_1}{\partial x_n}(\vec x) \
\frac{\partial f_2}{\partial x_1}(\vec x) & \frac{\partial f_2}{\partial x_2}(\vec x) & ... & \frac{\partial f_2}{\partial x_n}(\vec x) \
... & ... & ... & ... \ \frac{\partial f_m}{\partial x_1}(\vec x) & \frac{\partial f_m}{\partial x_2}(\vec x) & ... & \frac{\partial f_m}{\partial x_n}(\vec x) \ \end{pmatrix} $$ In dieser Matrix ist in einer Reihe alle möglichen partiellen Ableitungen für \(f_1(\vec x)\)
Nobla-Operator
Differentialoperatoren
Laplace
Gradient
Sei \(f: D \subset \R^n \to \R\) differenzierbar, dann heisst $$ \mathbf{grad} f(\vec x)=\grad f(\vec x)^T= \begin{pmatrix} \partial_{x_1} f(\vec x) \ \vdots\ \partial_{x_n}f(\vec x) \end{pmatrix} $$ der Gradient von \(f\).
Divergenz
Folgendes ist ein Beispiel: $$ \vec F : \Omega \sub \R^u \to \R^u & \vec F(\vec x)= \begin{pmatrix} F_1(\vec x)\ \vdots\ F_n(\vec x) \end{pmatrix} \ \mathrm{div} \vec F(\vec x) = \part_{x_1}F_1(\vec x) + \dots + \part_{x_n}F_n(\vec x) \ \begin{align} \mathrm{div}(\grad \vec F(\vec x))\ & = \part_{x_1}F_1(\vec x) + \dots + \part_{x_n}F_n(\vec x) \ &= \part_{x_1}\part_{x_1}F_1(\vec x) +\part_{x_2}\part_{x_2}F_1(\vec x) + \dots + \part_{x_n}\part_{x_n}F_n(\vec x) \ &= \part_{x_1^2}F_1(\vec x) + \dots + \part_{x_n^2}F_n(\vec x) \end{align} $$ Wenn die Divergenz
- positiv ist, dann steigt etwas (z.B. Raum wird wärmer)
- \(=0\) ist, dann bleibt sie gleich,
- negative ist, dann sinkt etwas (z.B. Raum wird kälter)
Rotation (curl in Englisch)
Satz von Gauss
Der linke Teil stellt ein abgeschlossenes Gebiet, der rechte Teil ist die Oberfläche von \(\Omega\).
FEM
- Multiplikation mit Testfunktion \(v(x)\)
- Partiel integrieren \(v(0)=v(1)=0\) gilt immer da es in den Funktionesraum \(V\) so eingebaut wird
Extremum & Infimum
Wenn eine Menge als \(]a, b[=(a, b) \in \R\) definiert ist, dann gibt es kein minimum und maximum. Anstelle, gibt es ein das Extremum (max) und das Infimum (min), welche angenähert werden aber nie getroffen werden. $$ \sup_{x\in]a,b[\in \R}=b \ \inf_{x\in]a, b[\in \R}=a $$