Reibung

Trockene Reibung

$$ F_R=\mu F_N \ F_N=m\cdot g $$ Die Reibungskraft $F_R$ ist proportional zur Normalkraft $F_N$ mit dem Faktor des Gleitreibungskoeffizient $\mu$.

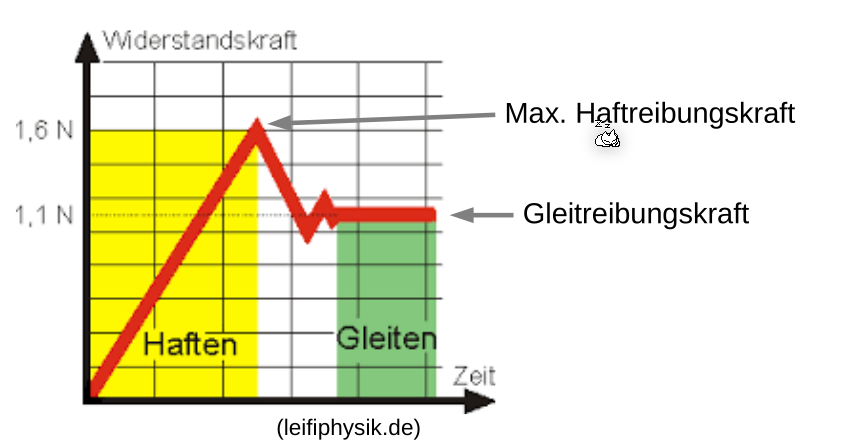
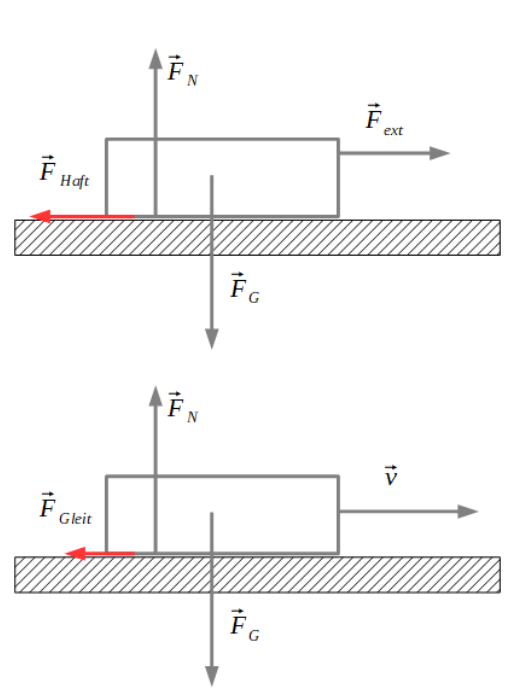
Wenn eine Masse sich nicht bewegt, wirkt die Haftreibungskraft $\vec F_{Haft}$. Sobald sich die Masse sich bewegt gilt die Gleitreibungskraft $\vec F_{Gleit}$. $\vec F_{Haft}$ und $\vec F_{Gleit}$ unterscheiden sich nur durch den Gleitreibungskoeffizient $\mu$.

Das Vorzeichen ist wichtig zu beachten. Es zeigt immer in die entgegengesetzte Richtung, in welche sich eine Masse bewegt.

Beispiel: Bei welchem Winkel?

Um den Winkel zu finden, bei dem eine Masse anfängt sich zu bewegen, kann $F_{Haft}=F_g$ gleich geseetzt werden: $$ \begin{align} F_{Haft}&=\mu\cdot m \cdot g \cdot \cos(\alpha)\ F_g&=m\cdot g \cdot \sin(\alpha)\ F_{Haft}&=F_g \ \mu \cdot m \cdot g \cos(\alpha)&=m \cdot g \cdot \sin(\alpha)\ \mu \cdot \cos(\alpha) &= \sin(\alpha)\ \alpha &= \frac{\sin(\alpha)}{\cos(\alpha)}\ &= \tan^{-1}(\mu) \end{align} $$

Viskose Reibung

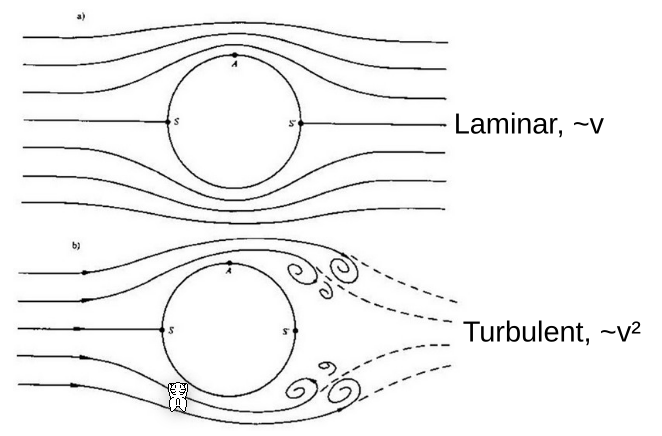
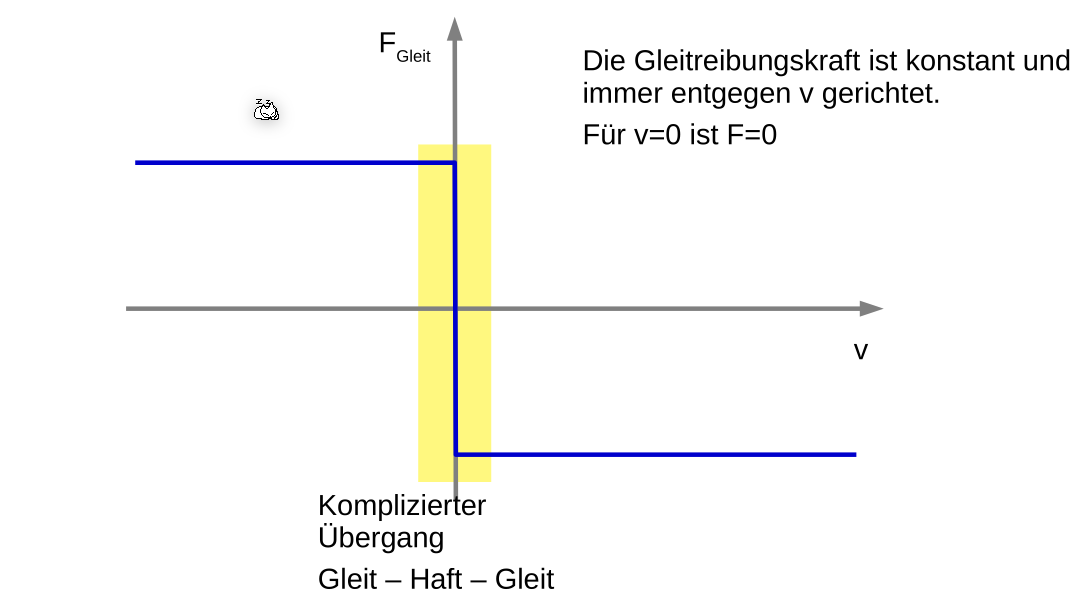
Es gibt zwei Arten von viskosen Reibung: Die laminare Strömung ist linear-proportional mit $v$. Wenn die Strömung turbulent ist, wie fast immer in der Realität, nimmt die Reibung quadratisch mit $v$ zu.

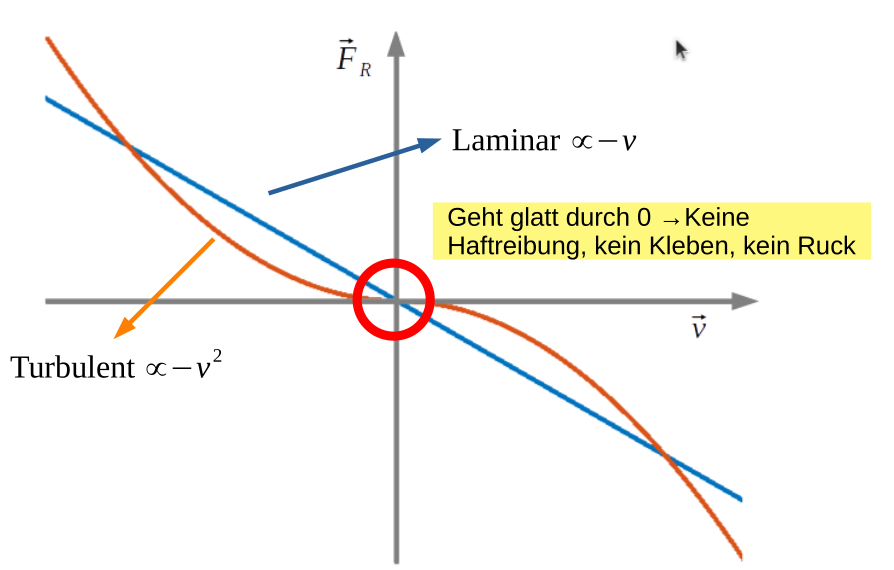
Die Reibungskraft bei turbulenten Strömen sieht folgendermassen aus: $$ \vec F_R = - \frac 1 2 \rho A c_w |\vec v|^2 \cdot \vec e_v $$ Dabei ist in dieser Formel die Dichte des Mediums $\rho$, die Stirnfläche der Masse $A$, ein Wiederstandsbeiwert $c_w$ und die Geschwindigkeit $\vec v$.