Model Selection

The goal of model selection is to find good hyperparameters for a given algorithm

Hyperparameters and Normal Parameters

Hyperparameters are parameters which aren't minimised by the cost function (e.g. when using gradient descent).

Hyperparameter Tuning

Here are some general approaches:

Manually setting the hyperparameters
Grid Search Search all combinations of hyperparameters in specified ranges
Randomised Search Train models on random hyperparameter combinations
Genetic Algorithms Using an algorithm, which does the selection, crossover and mutation steps to improve the hyperparameters

Data Split

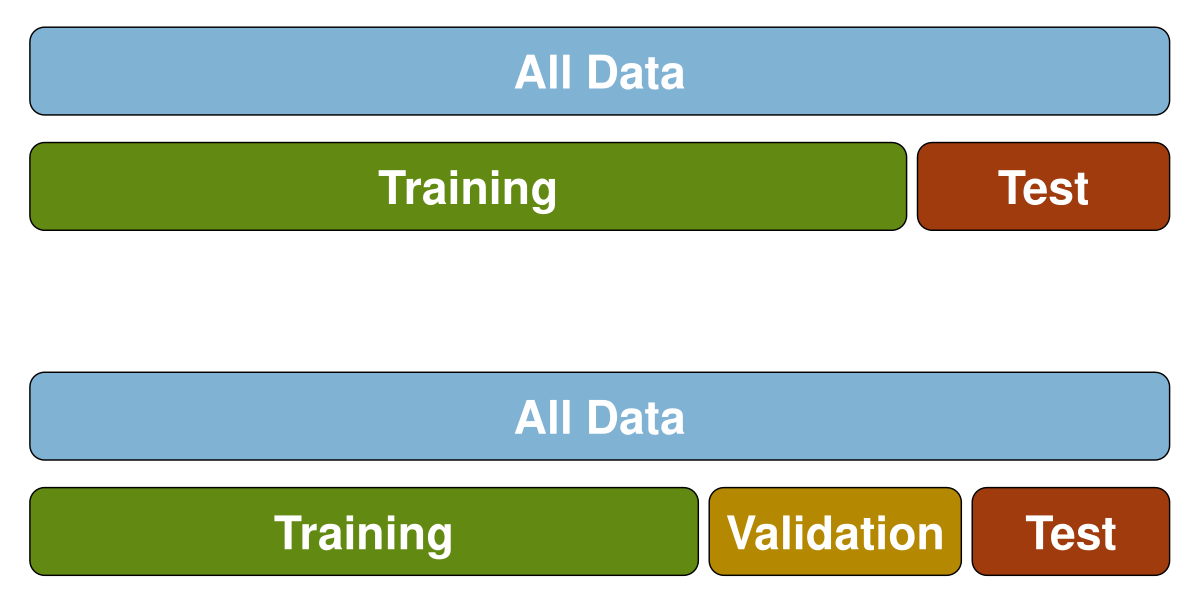
If we want to also tune hyperparameters of a model, we need an independent validation set. This needs to be independent, as the model shouldn't interact at all with the test set.

k-Fold Cross-Validation

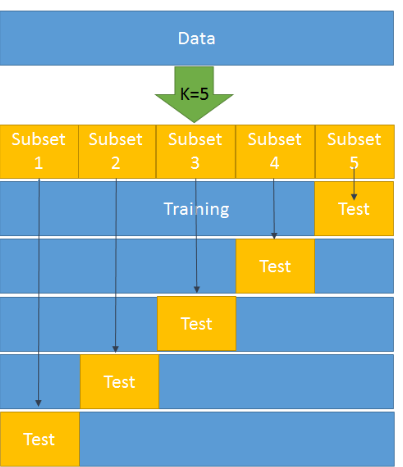
With k-fold cross-validation, we split the training set in to multiple approximately equally sized subsets. We then go through all subsets and use it as a test set and the rest as the training set. Afterwards we have \(n\) subsets of metrics (and also parameters). The values of the metrics are summed up and are the k-fold cross-validation score.

k-fold-validation is only used for hyperparameter tuning by optimising for the best k-fold cross-validation score. With those found hyperparameter, one can train the model and determine the best parameters.

This is also called leave-one-out cross-validation (LOOCV) if we have \(n\) samples and use \(n\) folds. This results in \(1\) test sample and \(n-1\) training samples for each fold.

After the k-fold-validation the entire training set can be used to train the mod

Stratified Sampling

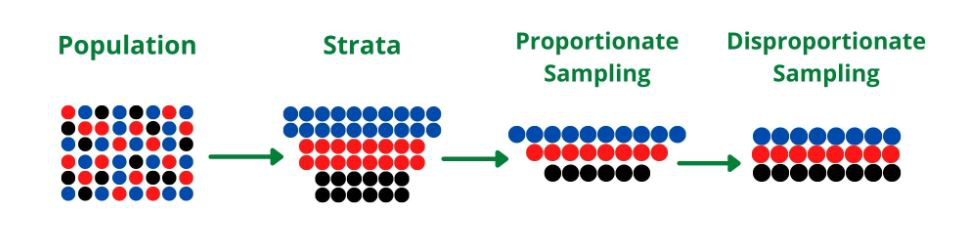
When having data with rare classes, this inbalance can effect the learning. To prevent this, the data can be sorted by its class and then sample from each class independently.

If this is done proportionally to the size of the class, it is called Proportionate Sampling, otherwise it is Disproportionate sampling.

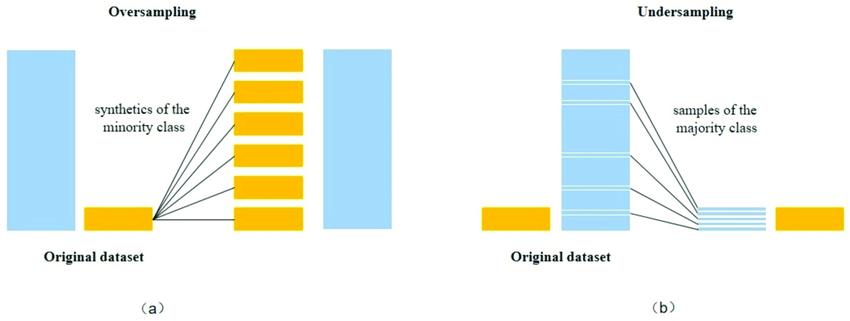
Oversampling

When oversampling, new data samples are created in minority classes. This can be done, by copying or modifying existing samples.

However, when copying existing samples, one has to pay attention that the model doesn't overfit. This risk can be mitigated by obtaining new data similar to existing data.

Undersampling

When undersampling, randomly, only a few samples from the original data sets are used for training.

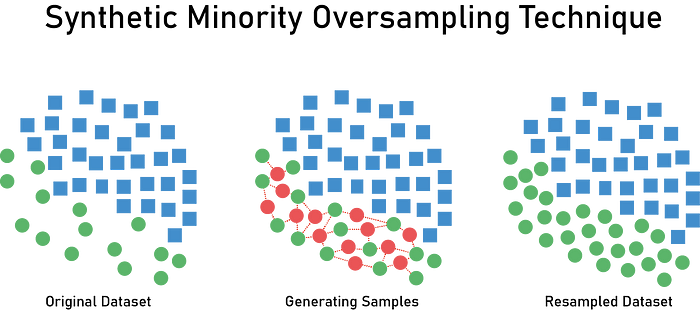
SMOTE

For minority categories, the algorithm selects a random samples from this group and calculates their \(k\) nearest neighbour.

SMOTE together with under sampling performs better then just under sampling.

Learning Curves

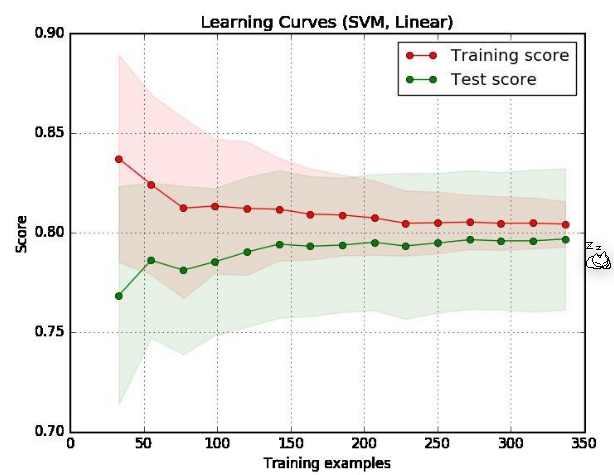
If both curves are close to each other and both of them have a low score then there is a potential underfitting. This means that the model should be complexer to handle the data.
If the training curve has a much better score than the testing curve then there is a potential overfitting (High Variance)

Examples:

The model is too simple to detect the patterns of the data. The model should be made more complex
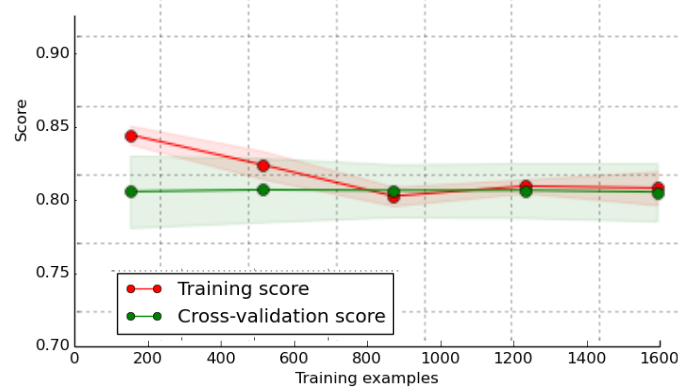
With this example, there is likely a high variance, overfitting is happening and the mode should be simplified. This is also called regularisation.

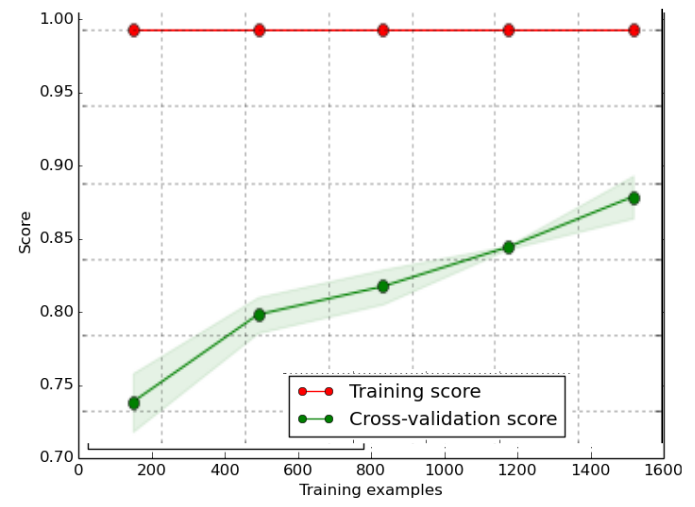
(In this example the cross-validation score can be used as a proxy for the test score)

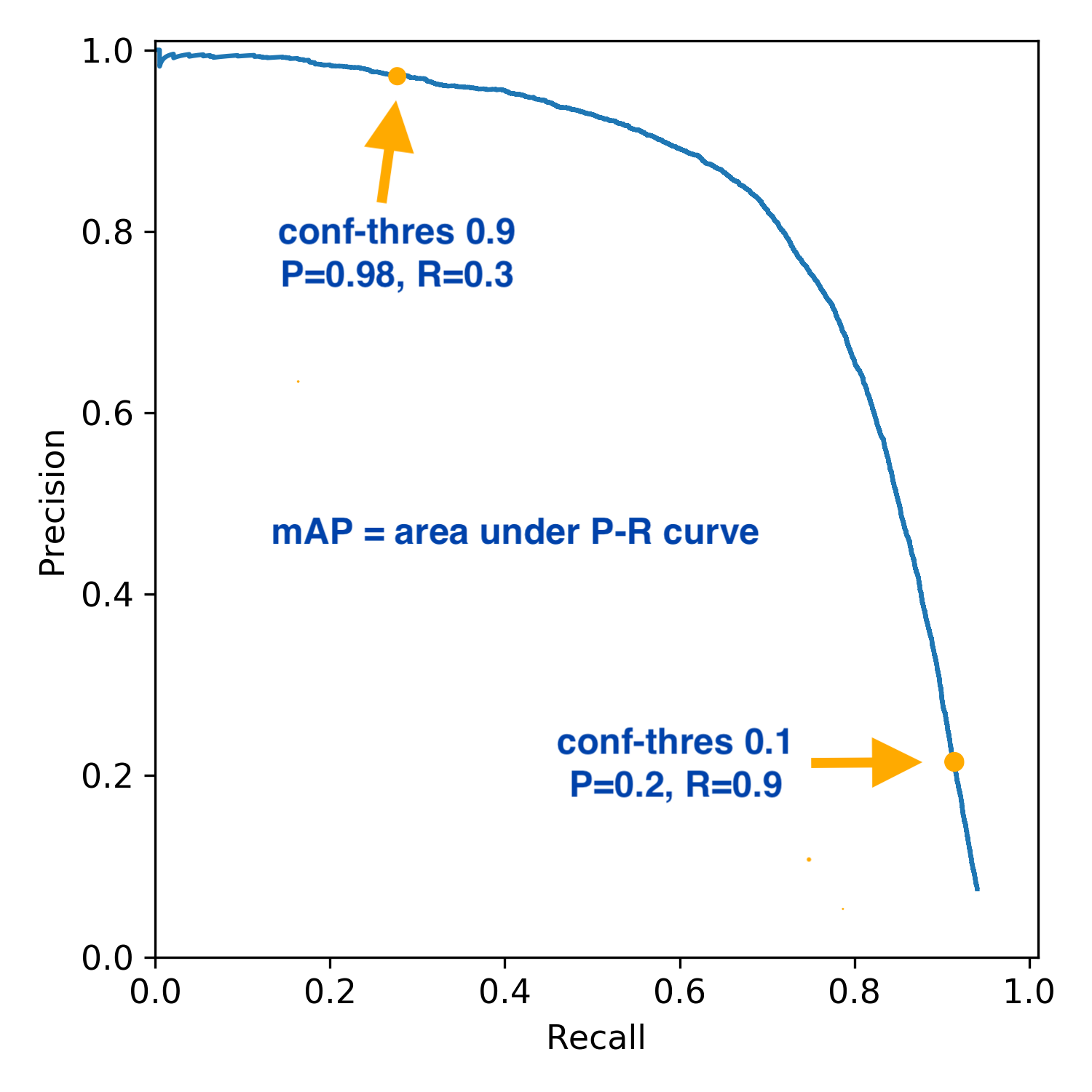
Precision vs Recall

This graph shows the trade of between precision and recall.