Lineare Gleichungssystem
Eine Gleichung ist lineare, wenn sie die folgende Form entspricht: \(ax+by+cz=d\)
Koeffizienten Matrix
Ein lineares Gleichungssystem kann als eine Matrize Multiplikation geschrieben werden. $$ \text{} \begin{cases} i_1x+i_2y=c_1\ i_3x+i_4y=c_2\ i_5x+i_6y=c_2 \end{cases} \ \begin{pmatrix} i_1 & i_2 \ i_3 & i_4\ i_5 & i_6 \end{pmatrix} \cdot \begin{pmatrix} x \ y \end{pmatrix} = \begin{pmatrix} i_1x+i_2y\ i_3x+i_4y\ i_5x+i_5y \end{pmatrix} = \begin{pmatrix} c_1\ c_2\ c_3 \end{pmatrix} $$ Dies kann vereinfacht als eine erweiterte Koeffizienten Matrix geschreiben werden: $$ \left( \begin{array}{cc|cr} i_1 & i_2 & c_1\ i_3 & i_4 & c_2\ i_5 & i_6 & c_3 \end{array} \right) $$
Homogene Gleichungssysteme
Homogene Gleichungssysteme sind Gleichungssysteme bei denen das Resultat bei allen Gleichungen 0 ist. Es kann eine oder unendlich viele Lösungen haben. Es ist nicht möglich, dass es keine Lösung hat.
Zeilenstufenform
Die Zeilenstufenform ist definiert durch die folgenden Regeln:
- Alle Zeilen mit nur
0stehen zu unterst - Wenn eine Zeile nicht nur aus
0besteht, ist die erste Zahl, welche keine0ist, eine1. Diese1wird als führende Eins bezeichnet - Eine führende Eins, welche weiter unten steht, muss auch weiter rechts stehen, als die anderen führenden Einsen
Zusätzlich gibt es noch die reduzierte Zeilenstufenform, bei welcher noch die Regel gilt, dass in den Spalten mit einer führenden Eins, die weiteren Elemente 0 sein müssen.
Bei der erweiterten Koeffizientenmatrix sind die Resultat-Werte (die \(c_i\) Werte) von den Regel ausgenommen werden.
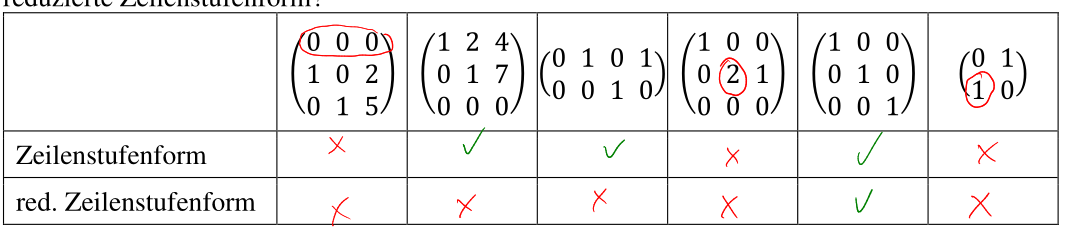
Folgendes Matrix ist in der Zeilenstufenform: 
Lösung aus der Zeilenstufenform
Um aus einer Zeilenstufenform die Lösung zu lesen, werden die Variablen in führende Unbekannte und freie Unbekannte unterteilt. Führende Unbekannte sind all diese Variable, welche in ihrer Spalte eine führende 1 haben, die anderen Variablen sind freie Unbekannte.

Für die freien Unbekannte werden nun eine beliebige Variable gleichgesetzt. Oft werden grichische Buchstaben verwendet, um die Verwechslungsgefahr gering zu halten.
Im oberen Beispiel: $$ x_2=\lambda\ x_4=\mu $$ Jede führende Unbekannte wird nun
in eine Gleichung übersetzt. Wieder für das Beispiel oben: $$ x_1-2x_2+3x_4=5 \rightarrow x_1=5+2x_2-3x_4\ x3-x4=3\rightarrow x_3=3+x_4 $$ Nun kann das Gleichungssystem von unten (also \(x_4\) in diesem Fall) gelöst werden: $$ \begin{align} x_4&=\mu\ x_3&=3+\mu\ x_2&=\lambda\ x_1&=5+2\lambda-3\mu \end{align} $$ In diesem Fall gibt es zwei Unbekannte \(\lambda\) und \(\mu\). Dank diesen gibt es unendlich viele Lösungen. Es kann auch eine spezifische Lösung oder gar keine Lösung geben.
Parameterdarstellung
Die Parameterdarstellung ist eine alternative Darstellungsmöglichkeit von des Resultats. Das untere Beispiel zeigt das Beispiels-Gleichungssystem von oben:
$$
\vec x=\begin{pmatrix}x_1\x_2\x_3\_x4\end{pmatrix}=
\begin{pmatrix}5 \0\3\0\end{pmatrix} +\lambda \begin{pmatrix}2\1\0\0\end{pmatrix}+
\mu\begin{pmatrix}-3\0\1\1\end{pmatrix}
$$
Anzumerken ist, dass \(x_2\) bei der \(\lambda\) Matrix ein 1 hat. Dies liegt daran, dass \(x_2=\lambda\) ist. Dasselbe gilt auch mit \(x_4=\mu\) und der \(\mu\) Spalte bei \(x_4\)
Zeilenstufenform herleiten (Gauss-Verfahren und Gauss-Jordan-Verfahren)
Ein Gleichungssystem, welches bereits in der Zeilenstufenform ist zu lösen, ist einfach. Die Frage ist nun, wie jemand ein solches Form herleiten kann.
- Wir nennen die am weitesten links stehende Spalte mit Element \(\neq0\) Pivot-Spalte
- Wenn die Zeile mit dem führenden Eins nicht zu oberst ist, wird sie mit der obersten Zeile getauscht
- Die oberste Zeile wird durch die erste Element \(\neq 0\) in der Spalte geteilt. So wird eine führende Eins erzeugt
- Um
0in der Pivot-Spalte unter der obersten Zeile zu erzeugen, wird jede Zeile unter der obersten Zeile mit einem Vielfachen der obersten Zeile addiert um0zu forderst zu erzeugen - Schritte 1-5 wiederholen, bis eine Zeilenstufenform vorhanden ist
Wenn eine reduzierte Zeilenstufenform verlangt wird, muss danach ein Vielfaches der unterste Zeile auf die oberen Zeile addiert werden, so dass diese 0 ergeben. Wenn man mithilfe der reduzierten Form die Gleichung löst, spricht man vom Gauss-Jordan-Verfahren, ansonsten nur vom Gauss-Verfahren.
Das folgende Beispiel wird an dem folgenden Gleichungssystem durchgeführt:
| Schritt | Beispiel |
|---|---|
| A1. Die erste Spalte ist die Pivot-Spalte A2. Das oberste Element der Pivot-Spalte ist bereits \(\neq 0\) A3. Es wird von der zweiten Zeile drei mal die erste Zeile abgezogen. Die dritte Zeile hat bereits eine 0 in der Pivot-Spalte |
$\left(\begin{array} {ccc |
| B1. Die zweite Spalte ist nun die Pivot-Spalte B2. Das oberste Element (die erste Zeile wird ignoriert, daher ist dies in der zweiten Zeile), ist eine 4, daher wird die zweite Zeile durch eine 4 geteilt |
$\left(\begin{array} {ccc |
| B3. Es wird das \((-1)\) Fache von der Zeile 2 zu der Zeile 3 addiert | $\left(\begin{array} {ccc |
| C1. Die dritte Spalte ist nun die Pivot-Spalte C2. Die ersten zwei Zeilen werden ignoriert, daher wird die letzte Zeile durch 2.75 geteilt, damit eine 1 zu forderst steht. |
$\left(\begin{array} {ccc |
Die Matrix ist nun in der Zeilenstufenform. Wenn die reduzierte Stufenzeilenform verlangt wird, muss der fünfte Schritt noch durch geführt werden:
| Schritt | Beispiel |
|---|---|
| A5. Die zweite Zeile wird mit dem \((-0.75)\) Fachen der Zeile drei addiert und die erste Zeile mit der Zeile drei addiert (also \(\cdot 1\)) | $\left(\begin{array} {ccc |
| B5. Die erste Zeile wird mit der zweiten Zeile addiert | $\left(\begin{array} {ccc |
Nun ist die Matrix in der reduzierten Zeilenstufenform.
Lösbarkeit von linearen Gleichungssystemen
Ein lineares Gleichungssystem hat drei verschiedene Lösungsmöglichkeiten: Keine Lösung, eine Lösung, unendliche Lösungen.
Graphisch gezeichnet, sieht dies so aus: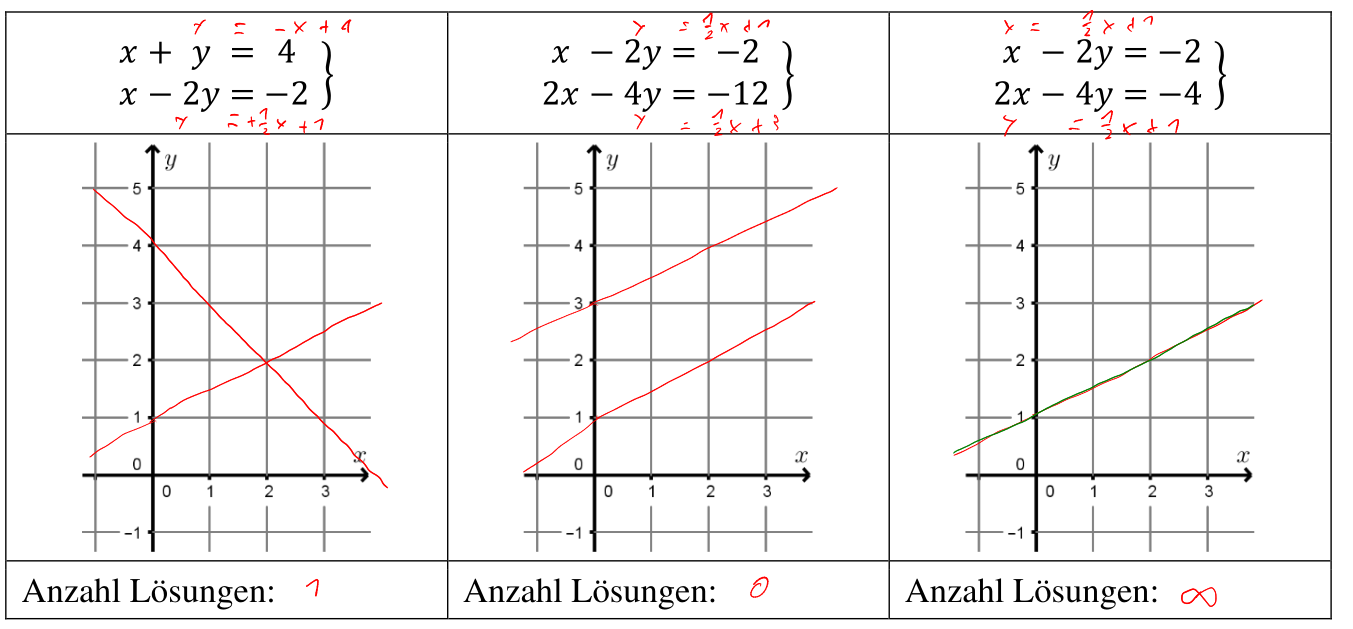
Um nicht jedes mal ein Gleichungssystem zeichen zu müssen, kann man den Rang des Gleichungssystems zu hilfe ziehen:
Der Rang \(rg(A)\) des Gleichungssystems \(A\) ist definiert als \(rg(A)=\text{Gesamtanzahl Zeilen} - \text{Anzahl Nullzeilen}\) in der Zeilenstufenform
\(rg(A)\) ist dabei die Matrix ohne die Koeffizienten \(\vec c\) (also ohne die Zahlen nach dem langen Strich). \(rg(A|\vec c)\) ist der Rang der kompletten Matrix (mit den Zahlen nach dem Strich inklusive)
- Ein lineares Gleichungssystem ist lösbar, wenn \(rg(A)=rg(A|\vec c)\)
- Es hat genau eine Lösung, wenn gilt: \(rg(A)=n\) , \(n\) ist die Anzahl Spalten von \(A\)
- Es hat unendlich viele Lösungen, wenn gilt: \(rg(A)<n\), \(n\) ist die Anzahl Spalten von \(A\)
Ein homogenes Gleichungssystem (alle Koeffizienten sind \(0\)) ist immer lösbar, da \(rg(A)=rg(A|\vec c)\) immer gilt.
Wenn mit Restklassen gearbeitet werden, kann es vorkommen, dass ein Gleichungssystem keine Lösung hat, da es kein multiplikatives Invers einer Restklasse gibt und somit die Zeilenstufenform nicht geformt werden kann.