Berechnungsmodelle

Church-Turning-These & Gandys These M

Intuitive berechenbare Funktion: eine Funktion, welche algorithmisch (durch eine mechanisches Verfahren) berechnet werden kann

Turing-berechenbare Funktionen: Funktionen, welche von einer Turing-Maschinen berechnet werden können

Jede intuitive berechenbare Funktion lässt sich mit einer Turingmaschine berechnen.

Gandys These M: Alles, was jemals mit einer (endlichen) Maschine/physikalischen Apparatur berechnet werden kann, ist bereits von einer Turing-Maschine berechenbar.

Bis jetzt wurde noch kein Gegenbeispiel zu beiden Thesen gefunden worden.

Turing-berechenbare Funktion

$u$ ist ein Wort. Pfeil noch oben ist nicht teil von $\Gamma$.

Oder: Wenn es eine Funktion gibt, welche für alle Input Wort anhält.

Beispiel

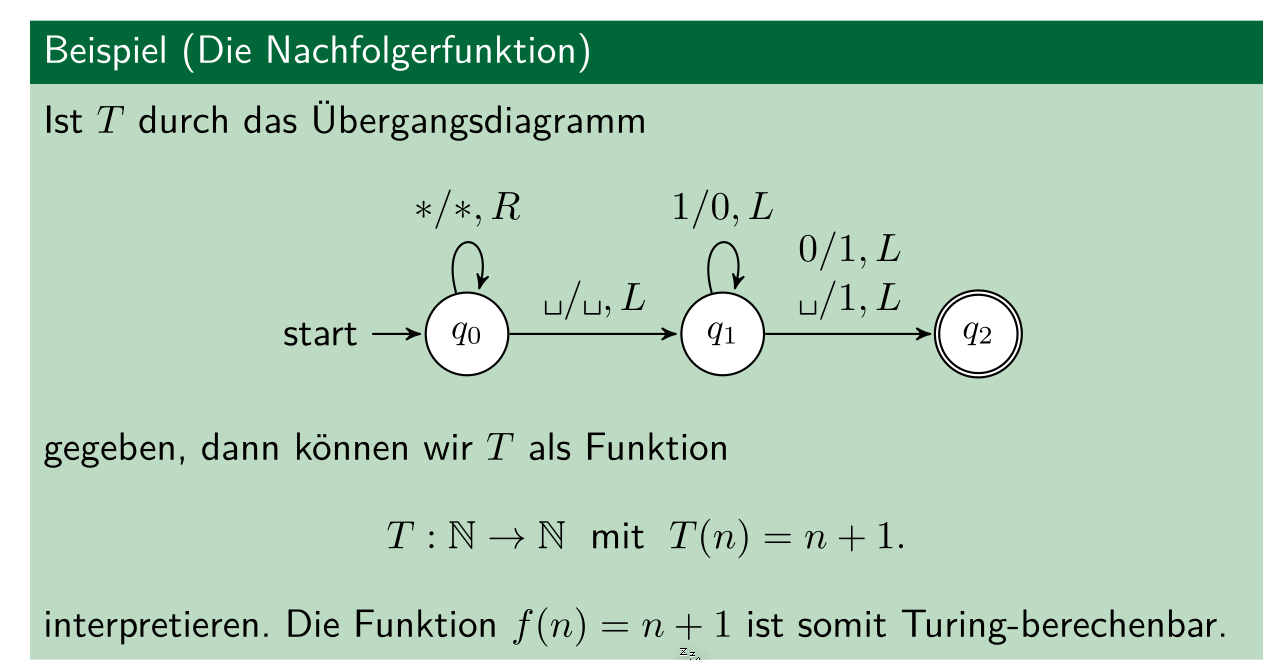
wenn zu 1011 1 addiert werden soll, wird so lange von rechts nach links gerückt, bis eine 0 gefunden wird. Diese wird zu einem 1 gemacht. Die 1 davor werden zu 0

Loop-Programme

Ein LOOP-Programm besteht aus folgendem:

Variabeln: $x_0$, $x_1$, $x_2$, ...,$x_k$

Konstante: 0, 1, 2, 3, ...

Zuweissungen: $x_k=x_j+c$ oder $x_k = x_j - c$

Wenn die Loop-Variable (x3 in LOOP x3 DO ... END) im Loop verändert wird, hat dies keinn Einfluss auf die Anzahl Durchläufe.

While-Programme

Turing-Vollständigkeit

Auch jede Turing-Maschine kann mit einem While-Programm implementiert werden.

GOTO-Programme

Primitiv rekursive Funktionen

Ackermannfunktion

Eine Ackermannfunktion $a: \N^2\rightarrow N$ ist durch die Gleichung: $$ \begin{align} a(0, m)&= m + 1\ a(n + 1, 0) &= a(n, 1)\ a(n + 1, m + 1) &= a(n, a(n + 1, m)) \end{align} $$

Loop-Interpreter

Ein Loop-Interpreter ist eine Funktion $I:\N\times \N \rightarrow \N$, welche als Input den Code und Input eines Loop-Programmes nimmt und den Code mit dem Input ausführt und zurück gibt. Für einen Loop-Interpreter gelten folgende Eigenschaften:

Es gibt genau ein totaler Loop-Interperter
Es kein Loop-berechenbare Loop-Interpreter. Es gibt also kein Loop-Programm, was Loop-Programme interpretieren kann