Parser

Context Free Grammar

SheepNoise -> SheepNoise baa 
            | baa

Formally a context-free grammar is a four tuple \(G = (S, N, T, P)\), where

• \(S\) is the start symbol
• \(N\) is a set of non-terminal symbol
• \(T\) is a set of terminal symbols
• \(P: N \to (N \cup T)^+\) is a set of productions/rewrite rules

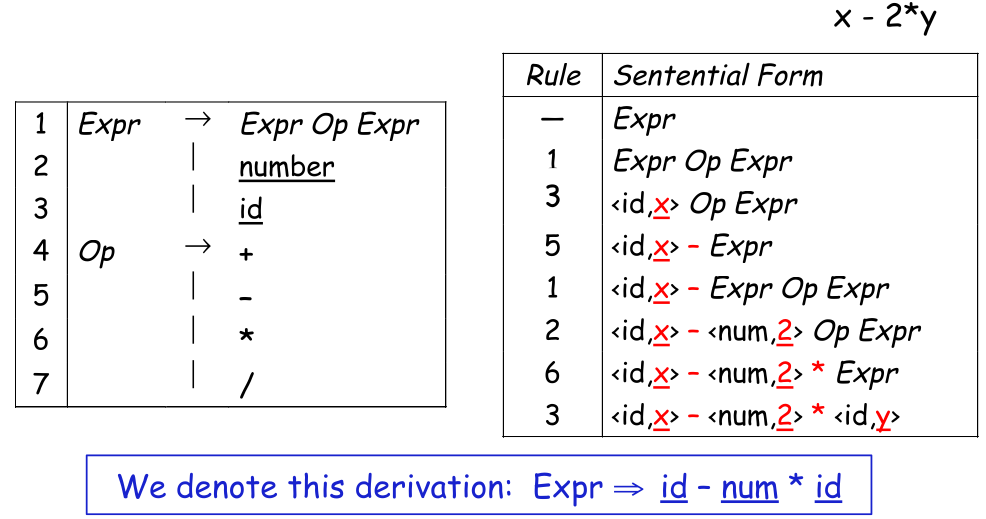
A sequence of rewrites is called a derivation, while the process of discovering a derivation is called parsing.

There are two kind of derivations:

• Leftmost derivation: replace the left most non-terminal symbol
• Rightmost derivation: replace the right most non-terminal symbol

A derivation can also be represented in a parse tree. A natural way to compute such a tree, is to walk it in post-order (visit children before the parent).

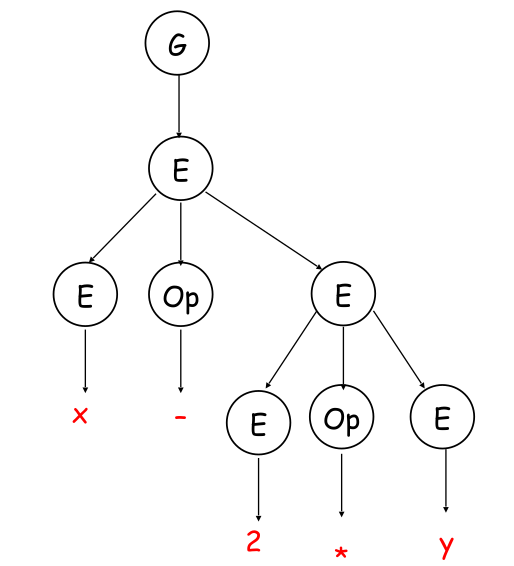
Precedence in Derivation

To add the precedence of operators to a grammar, there has to exist a non-terminal for each level of precedence. The parser then should recognise high precedence sub-expressions first.

A grammar for mathematical expression with precedence would look like the following:

Goal    -> Term
Expr    -> Expr + Term
        |  Expr - Term
        |  Term
Term    -> Term * Factor
        |  Term / Factor
        |  Factor
Factor  -> <number>
        |  <id>

The following is the leftmost derivation of the above rules of x - 2 * y:

- Goal
1 Expr
3 Expr - Term
4 Term - Term
7 Factor - Term
9 <id> - Term
5 <id> - Term * Factor
7 <id> - Factor * Factor
8 <id> - <number> * Factor
9 <id> - <number> * <id>

Ambiguous Grammar

Stmt    -> "if" Expr "then" Stmt
         | "if" Expr "then" Stmt "else" Stmt

With the above grammar, both example 1 and example 2 would be valid derivations

// example 1
if Expr1
    then if Expr2
        then Assignment1
        else Asignment2

// example 2
if Expr1
    then if Expr2
        then Assignment1
    else Asignment2

A way to disambiguate this, is the following grammar:

Stmt    -> "if" Expr "then" Stmt
         | "if" Expr "then" WithElse "else" Stmt
         | OtherStmt
WithElse -> "if" Expr "then" WithElse "else" Stmt
          | OtherStmt

Deeper Ambiguity

A deeper ambiguity like in Matlab a = f(17) f could be a function or an array. However, this kind of deeper context-sensitive ambiguity cannot be solved in a grammar and need to be solved at a later pass in the compiler.

Parser Implementation

• LL = Left-to-right scanning, Leftmost derivation
• LR = Left-to-right scanning, Rightmost derivation
• LL(1) is a grammar with one look-adhead token
• \(LL(1) \subset LR(1)\) (LL(1) is the superset of LR(1))

Top-Down Parser

1. Construct the root node of the parse tree
2. Repeat the following steps
3. At a node \(A\), select a production with \(A\) on its left-hand side and, for each symbol on its right-hand side, construct the appropriate child
4. When a terminal symbol is added to the fringe and it doesn't match the fringe of input, backtrack
5. Find the next node to be expanded

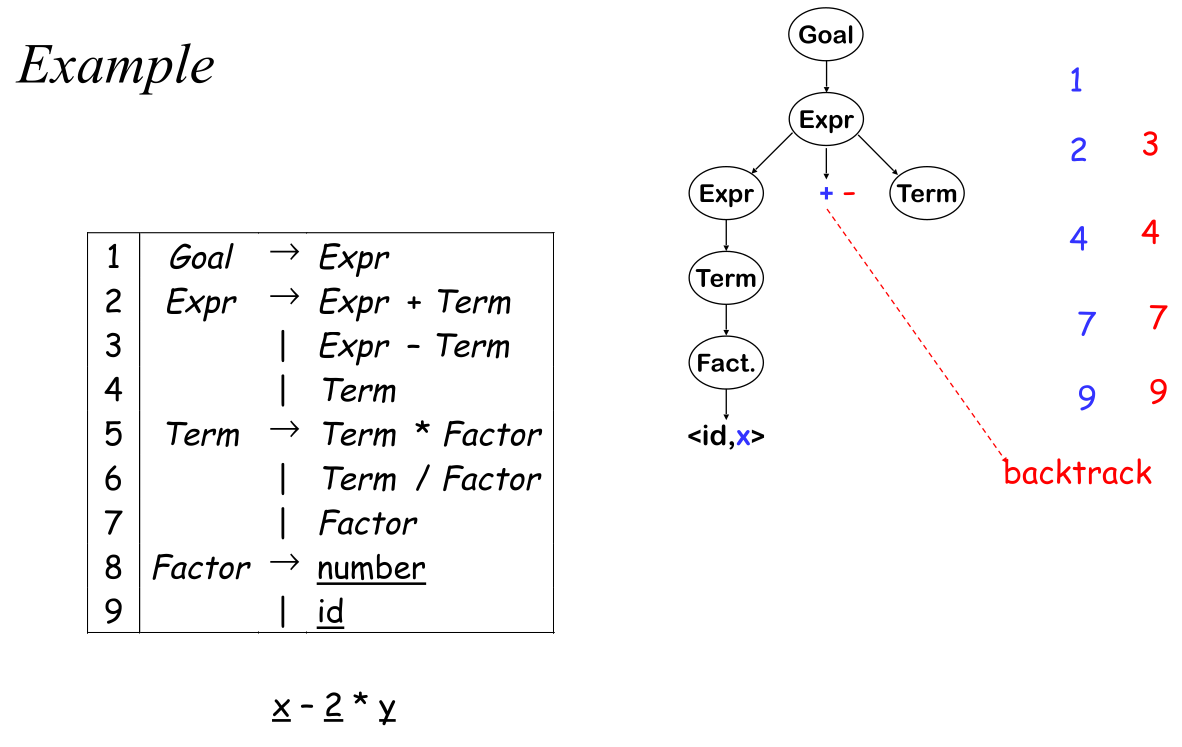
Another possibility to derive the grammar can lead to an infinite loop.

A top-down parser cannot parse a left-recursion since it uses the leftmost derivation. However, a top down parser can handle right recursive grammars.

Convert Left Recursion to Right Recursion

The following rule can be rewritten:

Fee -> Fee "+"
     | "-"

The rule above can be rewritten into the following:

Fee -> "-" Fie
Fie -> "+" Fie
     | ""       // empty string

Both of these grammar accept the same input, but the latter one is right recursive and can be parsed by a top down parser.

An algorithm to eliminate left recursion is:

1. arrange the non-terminals into some order \(A_1, A_2, ..., A_n\)
2. for \(i \leftarrow 1\) to \(n\)
3. for \(s \leftarrow 1\) to \(i - 1\)
   1. replace each production \(A_i \to A_s\gamma\) with \(A_i \to \delta_1 \gamma \mid \delta_2\gamma \mid ... \mid \delta_k\gamma\), where \(A_s \to \delta_1 \mid \delta_2 \mid ... \mid \delta_k\) are all the current productions for \(A_s\)
4. rewrite the productions to eliminate any direct left recursion

(This assumes that the initial grammar has no cycles and no epsilon productions)

The following example has an indirect left recursion (E -> T -> E ~ T -> T ~ T -> E ~ T ~ T ...):

G -> E
E -> E + T
E -> T
T -> E ~ T
T -> "id"

Running the algorithm yields the following:

1. The order of the non-terminal symbols is: \(G, E, T\)
2. \(G\) isn't rewritten since they are no symbols before \(G\) and it isn't directly left recursive
3. \(E\) is rewritten to \(E \to T E'; E' \to T E' \mid \varepsilon\)
4. \(T\) follows \(A_i \to A_s\gamma\) it is subsituded by \(T \to T E' ~T\)
5. Additionally \(T\) has a direct recursion: \(T \to id T'; T' \to E' \sim T T'; T' \to \varepsilon\)

All of these rewrites and substitutions yield the following result:

G   -> E
E   -> T E'
E'  -> + T E'
E'  -> ""           // empty string
T   -> "id" T'
T'  -> E' ~ T T'
T'  -> ""           // empty string

To eliminiate \(\varepsilon\)-productions, one can replace the \(\varepsilon\)-production where it occures.

A -> Bb
B -> C
B -> a
B -> ""
// this can be written as
A -> Cb
A -> ab
A -> b

Another Example

A   -> B x
B   -> C y
C   -> A z | z

1. Order \(A, B, C\)

LL(1) Grammar

The set \(FIRST(\alpha)\) contains all the tokens which appear as the first symbol in some string that derives from \(\alpha\). This also includes \(\varepsilon\).

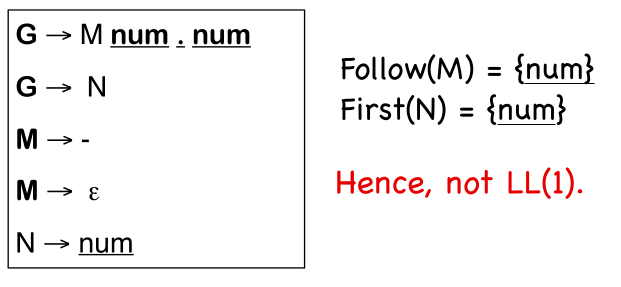
If \(A \to \alpha\) and \(A \to \beta\) both appear in the grammar, we would like \(FIRST(\alpha) \cup FIRST(\beta) = \{\}\). This allows the parser to make a correct choice with a look-ahead symbol of exactly one symbol, if there are no \(\varepsilon\)-productions.

If \(A \to \alpha\), \(A \to \beta\) and $\varepsilon \in FIRST(\alpha) $, then \(FIRST(\beta)\) needs to be disjointed from \(FOLLOW(\alpha)\) as well. \(FIRST^+(\alpha)\) is defined as \(FIRST(\alpha) \cup FOLLOW(\alpha)\) if \(\varepsilon \in FIRST(\alpha)\). Otherwise it is just \(FIRST(\alpha)\).

More formally, a grammar is \(LL(1)\) if \(FIRST^+(\alpha) \cup FIRST^+(\beta) = \{\}\) needs to hold.

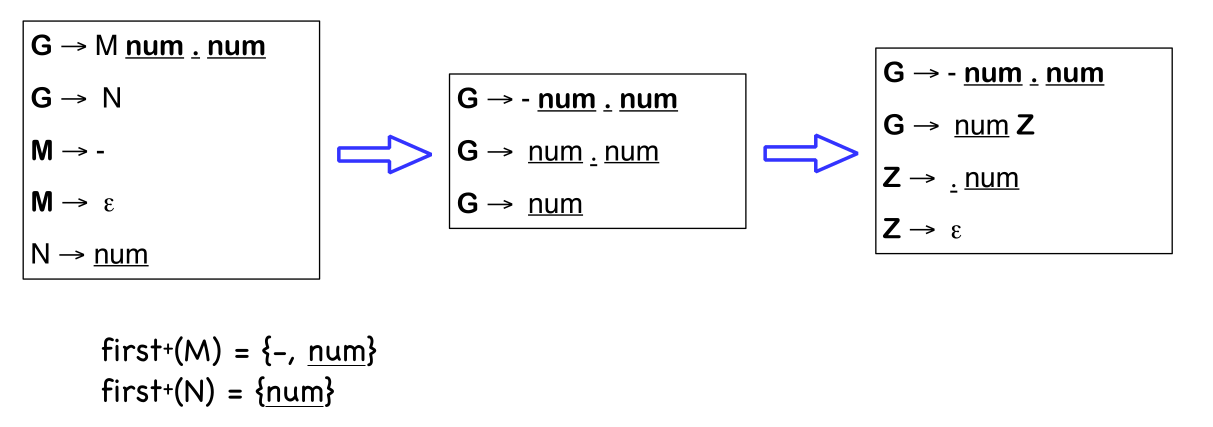
Left Factoring

A grammar can be transformed into a LL(1) grammar with the left factoring algorithm.

In the output of this algorithm, \(\varepsilon\)-productions are allowed.

1. \(\forall A \in NT\)
2. find the longest prefix \(\alpha\) that occurs in two or more right-hand sides of \(A\)
3. if \(\alpha \neq \varepsilon\) then replace all of the \(A\) productions \(A \to \alpha \beta_1 \mid \alpha \beta_2 \mid .. \mid \alpha \beta_n \mid \gamma\) with \(A \to \alpha Z \mid \gamma\) and \(Z \to \beta_1 \mid \beta_2 \mid ... \mid \beta_n\)
4. repeat until no common prefixes remain

A context free grammar which has the possibility to have an unbounded number of characters before the parser can decide to use \(A\) or \(B\), then the context free grammar cannot be an LL(1) grammar.

Recursive Decent Parsing

1. Build \(FIRST\) AND \(FOLLOW\) SETS
2. Massage grammar to have LL(1) condition
3. Remove left revursion
4. Left factor it
5. Define a procedure for each non-terminal
6. Implement a case for each right-hand side
7. Call procedures as needed for non-terminals
8. Add extra code, as needed
9. Perform context-sensitive checking
10. Build an IR to record the code

For a grammar like below, the parser would look like the following:

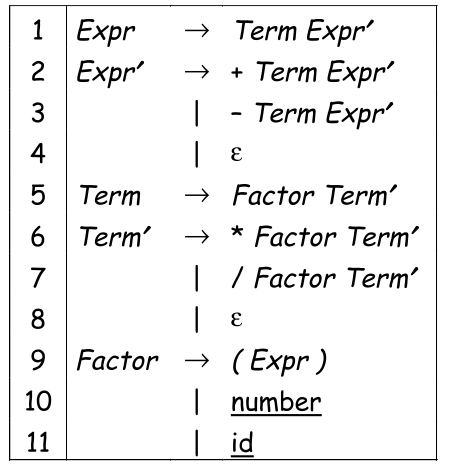
def Expr():
    if Term() == False: return False
    else: return EPrim()

def TPrime():
    if word == "*" or word == "/":
        word = NextWord()
        if Factor() == False:
            return False
        else: 
            return TPrime()

def Factor():
    if word == "(":
        word = NextWord()
        if Expr() == False:
            return False
        else:
            ...

Table-Driven Top-Down Parser

There is a table with a row for ever non-terminal and a column for every terminal.

To fill the table \(TABLE[X, y], X \in NT, y \in T\).

1. entry is the rule \(X \to \beta\), if \(y \in FIRST(\beta)\)
2. entry is the rule \(X\to \beta\), if \(y \in FOLLOW(X)\) and \(X\to\varepsilon \in G\)
3. otherwise, the entry is an error

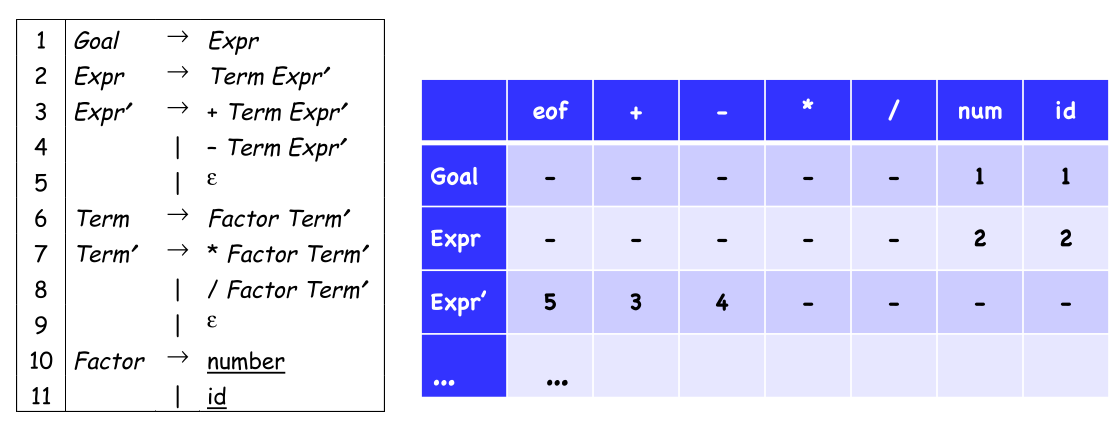
The following pseudo-code shows how the table is used:

token <- next_token()
push EOF onto stack
push the start symbol, S, onto the stack
TOS <- top of stack

loop forever {
    if(TOS == EOF && token == EOF) {
        report success
        break
    } else if(TOS is terminal) {
        if(TOS matches token) {
            pop stack
            token <- next_token()
        } else {
            report error looking for TOS
        }
    } else {
        if(TABLE[TOS, token] is (A -> B¹B²...B^k)) {
            pop stack
            push (B^k, ..., B²,B¹) # in that order
        } else {
            report error expanding TOS
        }
    }
        TOS <- top of stack
}

LR(1) Grammar

Bottom-Up LR(1) Parser

Bottom-up parsers use handles to decide which rule to use. A handle is a substring \(\beta\) in the right-hand side of some production \(A \to \beta\). A grammar \(G\) is unambiguous, if every sentential form in the rightmost derivation has a unique handle.

An LR(1) parsers are table-driven, shift-reduce parsers which look ahead one token to disambiguate reduce and shift actions. An LR(1) parser recognises languages that have an LR(1) grammar.

push INVALID
push start state;
token ← next_token( )
while (true) do;
    state ← top of stack;
    if Action[state, token] = “reduce A→β” then begin;
        pop 2x|β| symbols;
        state ← top of stack;
        push A;
        push Goto[state, A];
    end;
    else if Action[state,token] = “shift si” then begin;
        push token ;
        push si;
        token ← next_token( );
    end;
    else if Action[state, token] = “accept”
        then break;
    else Fail();
end;
report success;

(The reason why the token is pushed, is for book-keeping reason. Otherwise no parse tree could be generated. However, they are always pushed and popped in pairs and could also be represented as a tuple)

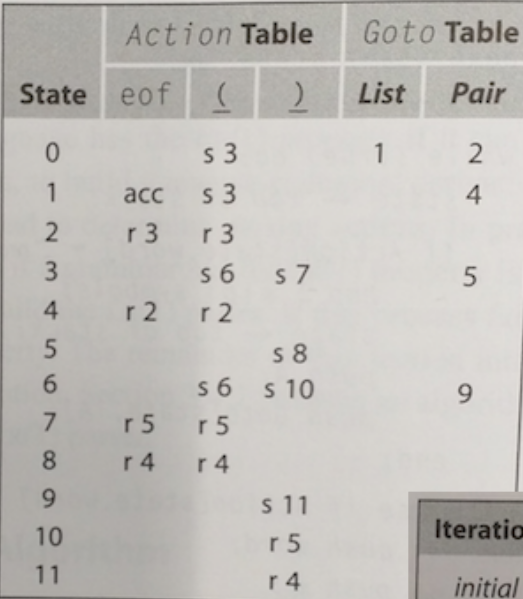
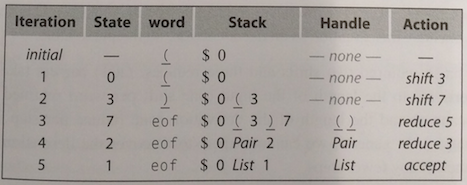
Build an AST during Parsing

Estimate Cycle Counts

Goal    -> Expr                 $$ = $1
Expr    -> Expr + Term          $$ = MakeAddNode($1, $3)
        |  Expr - Term          $$ = MakeSubNode($1, $3)
        |  Term                 $$ = $1

Term    -> Term * Factor        $$ = MakeMulNode($1, $3)
        |  Term / Factor        $$ = MakeDivNode($1, $3)
        |  Factor               $$ = $1      

Factor -> ( Expr )              $$ = MakeParNode($2)
        | number                $$ = MakeNumNode($1)      
        | id                    $$ = MakeIdNode($1)  

Build LR(1) Tables

There are two steps:

1. Determine the states from a given grammar
2. Fill the actions for each state into the ACTION-table, and fill the GOTO-table with the state-transitions following reductions

An LR(1) item \([A \to \beta \textbullet\gamma, a]\) represents that the parser is currently matching \(A\), has just parsed \(\Beta\) and expects to see \(\gamma\) next. The \(\textbullet\) represents where the parser currently is. \(a\) is what is expected after \(A\) has been matched. Each state is composed of multiple LR(1) items.

A master item is the initial state LR(1) item or an item directly derived from other states.

Help items are from the expasion of existing items and are used for deriving itmes of other states

The canonical collection is the set of all states

1. Begin with the initial state master item \([S' \to \textbullet S, EOF]\) and get its help items with the \(closure\)-function. The master item and its help item for the first state \(s_0\)
2. For each symbol in the grammar, compute the master items of the next state with the \(goto\)-function and get the help items with the \(closure\)-function. This forms the next state \(s_{next}\)

The \(closure(s)\) function:

1. while (\(s\) is still changing)
2. for each item \([A \to \beta \textbullet C\delta, a]\in s\)
   1. for each production \(C \to \gamma \in P\)
      1. for each \(b \in FIRST(\delta a)\)
         1. \(s \to s \cup \{[C \to \textbullet\gamma, b]\}\)
3. returns \(s\)

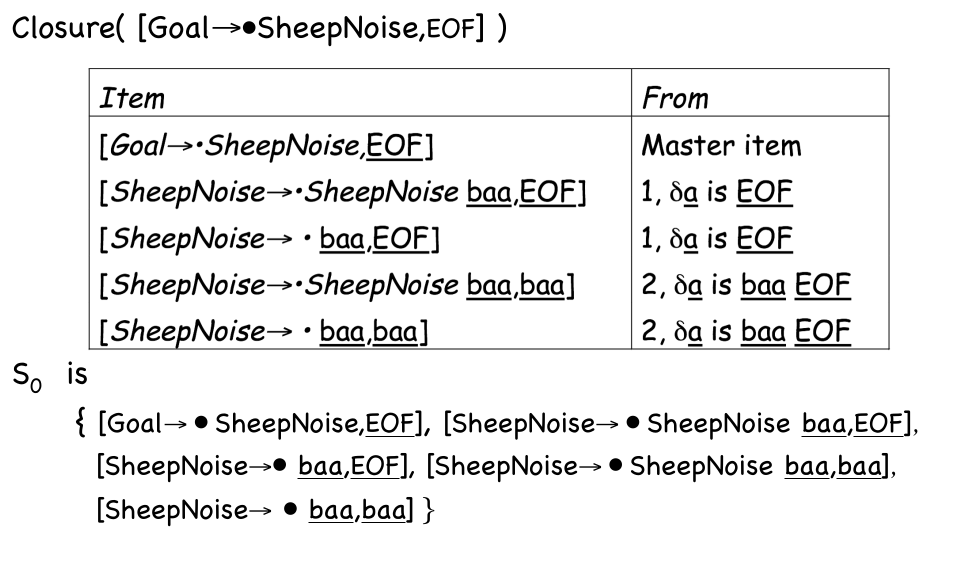
with the following grammar: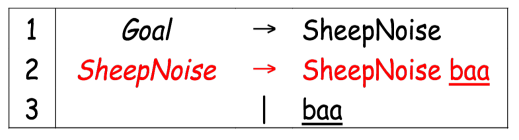

The \(goto(s, x)\) function:

1. \(moved \leftarrow \emptyset\)
2. for each item \(i \in s\)
3. if the form of \(i\) is \([\alpha \to \beta \textbullet x\delta, a]\) then
   1. \(moved \leftarrow moved \cup \{[\alpha \to \beta x \textbullet \delta, a]\}\)
4. return \(closure(moved)\)

To create all of the different states, the following algorithm can be used:

1. \(cc_0 \leftarrow \emptyset\)
2. for each production of the form \(Goal \to \alpha\) do
3. \(cc_0 \leftarrow cc_0 \cup \{Goal \to \textbullet \alpha, eof\}\)
4. \(cc_0 \leftarrow closure(cc_0)\)
5. \(CC \leftarrow \{cc_0\}\)
6. while (new sets are still being added to \(CC\)) do
7. for each unmarked set \(cc_i \in CC\) do
   1. mark \(cc_i\) as processed
   2. for each \(x\) following a \(\textbullet\) in an item in \(cc_i\) do
      1. \(temp \leftarrow goto(cc_i, x)\)
      2. if \(temp \notin CC then\)
         1. \(CC \leftarrow CC \cup \{temp\}\)
      3. record transition from \(cc_i\) to \(temp\) on \(x\)

To fill the action table, the following algorithm can be used:

1. for each state \(cc_i \in CC\)
2. for each item \(i \in cc_i\)
   1. if \(i\) is \([A \to \beta \textbullet c \gamma, a]\) and \(goto(cc_i, c) = cc_j\) then
      1. \(Action[i, c] \leftarrow \text{"shift }j\text{"}\)
   2. else if \(i\) is \([A \to \beta \textbullet, a]\) then
      1. \(Action[i, a] \leftarrow \text{"reduce } A \to B\text{"}\)
   3. else if \(i\) is \([Goal \to \beta \textbullet, eof]\) then
      1. \(Action[i, eof] \leftarrow \text{"accept"}\)
3. for each \(n \in NT\) do
   1. if \(goto(cc_i, n) = cc_j\) then
      1. $Goto[i, n] \leftarrow $j

Ad-Hock Translation

TODO

Attribute Grammar

(Note: The attribution rules for a production doesn't necessarily being run in sequence)

Circularity

A strongly non-circular grammar (SNC) is a grammar which can only generate instances with asyclic dependency graphs. This property can be tested in polynomial time. However, failing the test just means that it was inconclusive (not that the graph is not an SNC).

TODO: Insert of cyclic grammar