Vektorräume

Definition von Vektorräumen

Ein Vektorraum ist eine Menge $V$ mit den Funktionen Addition und Skalar-Multiplikation: $$ +:V \times V \rightarrow V\ \cdot : \R \times V \rightarrow V $$ Dabei müssen folgende Gesetze existieren:

Kommutativgesetz: $a + b = b + a$
Assoziativgesetzt: $a + (b + c)=(a + b) + c$
Es gibt ein neutrales Element $\vec 0$, für welches gilt $a + 0v = \vec a$ und $0v \in V$
Für jedes Element $a \in V$ muss es ein inverses Element $-a \in V$ geben, so dass $a + (-a) = 0v$ ergibt.
Assoziativgesetzt: $\lambda \cdot (\mu \cdot a) = (\lambda \cdot \mu) \cdot a$
Distributivgesetzt: $\lambda \cdot(a + b) = \lambda \cdot a + \lambda \cdot b$
Distirbutgesetzt: $(\lambda + \mu)\cdot a = \lambda \cdot a + \mu \cdot a$
Für jedes Element $a \in V$ gibt es ein neutrales Element $1\cdot a = a$,

Frage: muss das Skalar über $\R$ erstellt werden oder könnte auch eine andere Menge genommen werden.

Reeler Vektoraum

\[ +:V \times V \to V: (\vec a; \vec b) \mapsto \vec a + \vec b\\ \cdot : \R \times V \to V : (\lambda; \vec a) \mapsto \lambda \cdot \vec a \]

Das neutrale Element bei der Addition ist der Nullvektor $\vec 0$ und das neutrale Element bei der Skalarmultiplikation ist $1$.

Unterräume

Eine Teilmenge $U$ eines Vektorraums $V$ heisst Unterraum von $V$, wenn $U$ selbst auch ein Vektorraum ist. Dafür müssen folgende Kriterien erfüllt sein:

Für beliebige Element $a, b \in U$ ist auch $a+b\in U$
Für jeden Skalar $\lambda \in \R$ und jedes Element $a\in U$ ist auch $\lambda \cdot a\in U$
Die neutralen Elemente der Addition und Skalarmultiplikation müssen ebenfalls in $U$ sein.

Linearer Spann

$spann(\vec a_1, \vec a_2, ..., \vec a_n)$ ist definiert als alle möglichen Vektoren von der Linearkombination $\lambda_1\cdot \vec a_1 + \lambda_2\cdot \vec a_2 +...+\lambda_n\cdot \vec a_n$§

Die Vektoren $\vec a_1, \vec a_2, ...\vec a_n$ spannen den linearen Spann auf und formen eine geometrische Form.

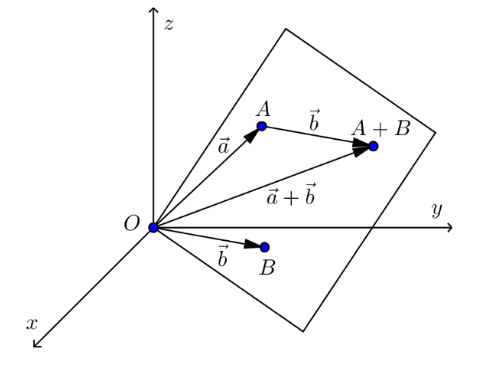
Geometrische Objekte

Jenachdem, wie viele Vektoren gegeben sind, wird ein anderes geometrisches Objekt gebildet:

Bei 1 Vektor, wird eine Ursprungs-Gerade gebildet
Bei 2 Vektoren, wird eine Ursprungs-Ebene
Bei 3 Vektoren, wird ein "Ursprungs-Körper" gebildet

Erzeugendensystem

Eine Menge von Vektoren $\{\vec b_1, \vec b_2, ..., \vec b_N\}$ bildet ein Erzeugendensystem von $V$, falls $V=span(\vec b_1, \vec b_2, ..., \vec b_n)$. Dies ist nur der Fall, wenn die Vektoren nicht kollinear, bzw. komplanar sind.

Aus dem gehen die folgenden folgende Bedingungen: $$ \begin{align} & V=span(\vec b_1, \vec b_2, ..., \vec b_n)\ \Leftrightarrow \text{ } & B\cdot \vec x = \vec a \text { für jedes } \vec a \in \R^m\ \Leftrightarrow \text{ } & rg(B)=m \end{align} $$

Mit den Vektoren $\vec b_i$ in einem Erzeugendensystem können alle anderen Vektor $V$ (also z.B. $\R^2$) bilden.

Basis und Dimensionen

Ein Vektor $\vec a = \pmatrix{a_1 \\ a_2}$ kann auch als $\vec a = a_1\cdot \vec e_1 + a_2 \cdot \vec e_2$ geschrieben werden. Anstatt der Vektormenge $\mathcal S=\{\vec e_1; \vec e_2\}$ kann auch eine andere Menge $\mathcal B=\{\vec b_1; \vec b_2\}$ benützt werden. Der Vektor $\vec a = \pmatrix{\alpha_1\\ \alpha_2}_\mathcal{B}$ ist nun equivalent zu $\vec a=\alpha_1 \cdot \vec b_1 + \alpha_2 \cdot \vec b_2$.

In diesem Beispiel sind die Vektoren $\vec a$, $\vec c$ und $\vec d$ die selben, nur die Vektormenge, durch welche das Koordinatensystem definiert wird, ändert sich.

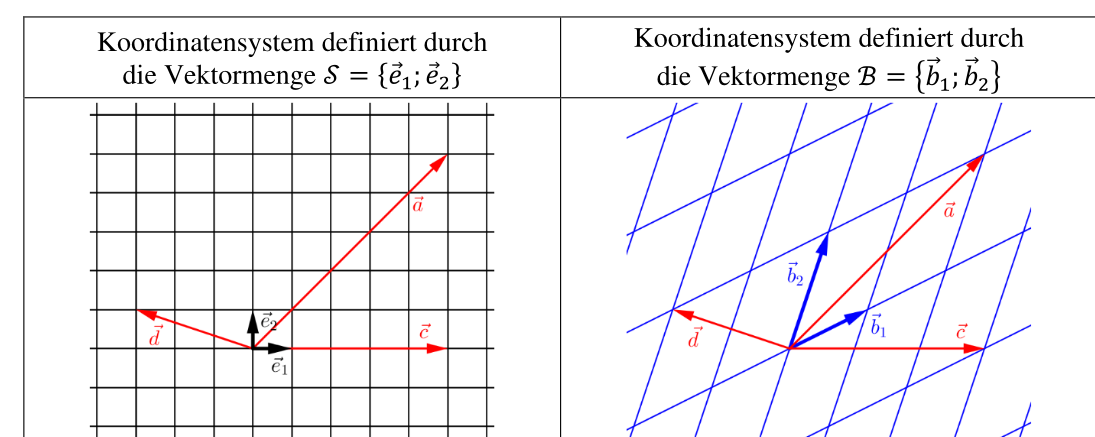
Damit dies möglich ist, muss die Vektormenge folgende Eigenschaften erfüllen:

$\mathcal B=\{\vec b_1, \vec b_2, ...,\vec b_n\}$ muss ein Erzeugendensystem sein
$\vec b_1$, $\vec b_2$, ..., $\vec b$ müssen linear unabhängig sein

Oder in Deutsch: Es darf nur genau eine mögliche Linearkombination für jeden Vektor geben

Aus diesen zwei Regeln gehen folgende Sätze hervor:

Eine Basis $\R^n$ besteht genau aus $n$ Vektoren
$\rm rg(B)=n$ (wobei $B$ alle Vektoren in eine Matrix gesteckt werden)
$\det(B)\neq 0$
$B$ ist invertierbar
Das lineare Gleichungssystem $B\cdot \vec x=\vec c$ hat genau eine eindeutige Lösung

Dimensionen

Die Dimension $\dim(V)$ gibt an, wie viel Dimensionen ein Vektorraum oder Basis hat.

Bei einer Basis $\mathcal B$ ist die Basis die Anzahl Vektoren, welche die Basis definiert. Das heisst $\dim(\R^n)=n$ und $\mathrm{dim}(\mathbb P_n[x])=n+1$

Bei einem Vektorraum ist die Anzahl Dimensionen gleich der Anzahl Vektoren, welche den Spann des Vektorraumes definieren. Bei Vektorräume gilt auch, dass ein Unterraum $R$ von $V$ : $\dim(R) \le \dim(V)$. Die Dimension des Vektorraums $\{\vec 0\}$ ist gleich $\dim(\{\vec 0\})=0$

TODO: Matrixen

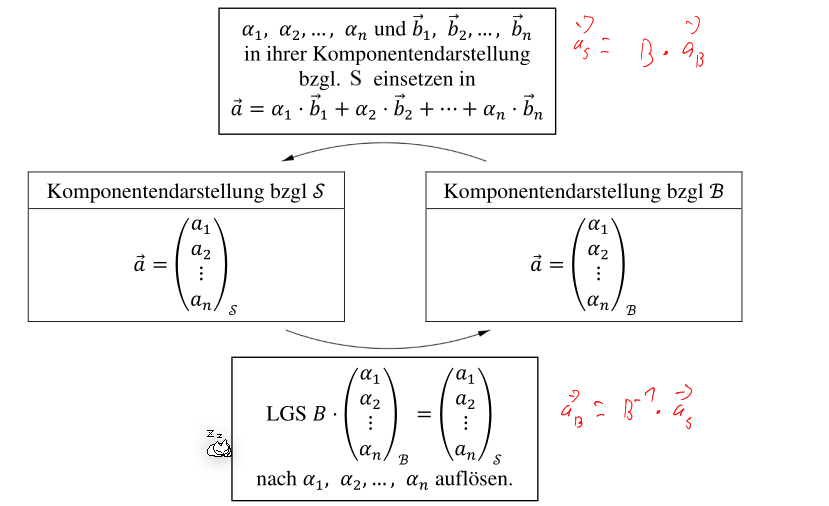
Umwandeln zwischen Komponentendarstellungen

Um einen Vektor $\vec v_{\mathcal B}$ in den Vektor $\vec v_{\mathcal{S}}$ zu umwandeln, kann folgendes getan werden: $\vec v_{\mathcal B}=v_1\cdot \vec b_1+v_2\cdot \vec b_2+...+v_n\cdot \vec b_n$

In die umgekehrte Richtung gibt es ein Lineares Gleichungssystem: $\vec v_\mathcal{S}\cdot B=\vec v_\mathcal{B}$