Differentialgleichungen

Eine gewöhnliche Differentialgleichung ist eine Gleichung, welche nur nach einer Variable abgeleitet wird: $$ \frac{\part y}{\part t} = f(t, y(t)) $$ Im oben Beispiel ist es eine gewöhnliche Differentialgleichung 1. Ordnung, da nur einmal Abgeleitet wurde.

Genereller ausgedrückt, folgendes ist eine gewöhnliche Differentialgleichung $n$-ter Ordnung: $$ y^{(n)}(x) = f(x, y(x), y'(x), ..., y^{(n-1)}(x)) $$ Eine allgemeine Lösung für eine Differentialgleichung $n$-ter Ordnung hat $n$ unabhängige Parameter (von den Integrationskonstanten).

Differentialgleichungen, welche die folgende Form haben $$ \frac{\part n}{\part t}=-\lambda n $$ haben die Lösung $n(t)$: $$ n(t)=n_0e^{-\lambda t} $$

Anfangswertproblem

Bei einem Anfangswertproblem wird, zusätzlich zu der Gleichung, den Funktionswert bei $x_0$, wie auch den Wert für jede benützte Ableitung bei dem selben Wert $x_0$.

Als Beispiel für folgende Funktion $s$ wird $C_1$ und $C_2$ benötigt, damit ein Resultat berechnet werden kann. Es wird also $s(t=0)$ und $s'(t=0)$ benötigt, um das Anfangswertproblem zu lösen. $$ s''=g\ s(t)=\frac 1 2 g t^2 + C_1t + C_2\ s(t=0)=C_2\ s'(t=0)=v(t=0)=C_1 $$

Richtungsfelder

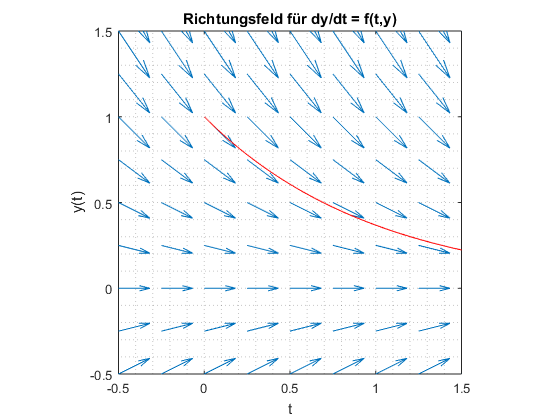
Ein Richtungsfeld stellt die Steigung als Pfeile dar. Dafür wurde in diesem Beispiel alle $y'$ für alle Punkte berechnet und eingezeichnet.

Eulerverfahren

Klassisch

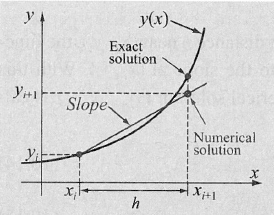
Um eine Lösung für eine Differentialgleichung mit einem Richtungsfeld zu finden, kann eine Schrittweite $h$ definiert werden. Jeder Punkt $(x_i, y_i)$ soll nun den Pfeilen im Feld folgen. Dies kann folgendermassen für eine Differentialgleichung $y'=f(x, y)$ erledigt werden: $$ \begin{align} x_{i+1} &= x_i + h\ y_{i+1} &= y_i + y' \cdot h \ &= y_i + f(x_i, y_i) \cdot h \end{align} $$ Zusätzlich wird auch noch ein Startpunkt $(x_0, y_0)$ benötigt.

Mittelpunkt

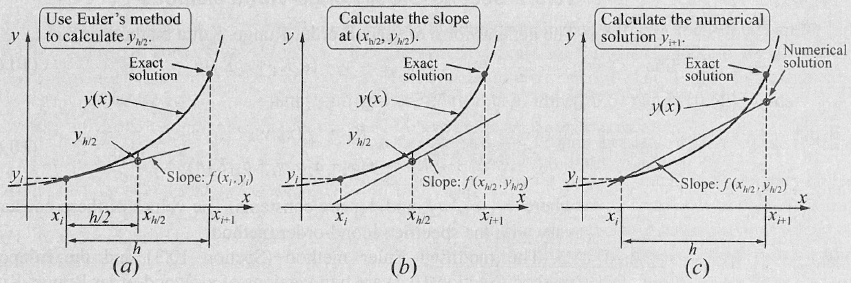
Im Vergleich zum Eulerverfahren, wo die Steigung beim Punkt $(x_i, y_i)$ berechnet wird, wird beim Mittelpunkt-Verfahren die Steigung bei $(x_i+\frac h 2, y_i + \frac h 2)$ berechnet.

Dafür muss aber der Punkt $(x_i+\frac h 2, y_i + \frac h 2)$ zuerst berechnet werden. Daher ergibt sich folgendes: $$ \begin{align} x_{h/2} &= x_i + \frac h 2\ y_{h/2} &= y_i + \frac h 2 \cdot f(x_i, y_i)\ \ x_{i+1} &= x_i + h\ y_{i+1} &= y_i + f(x_{h/2}, y_{h/2}) \cdot h \end{align} $$

Modifiziert

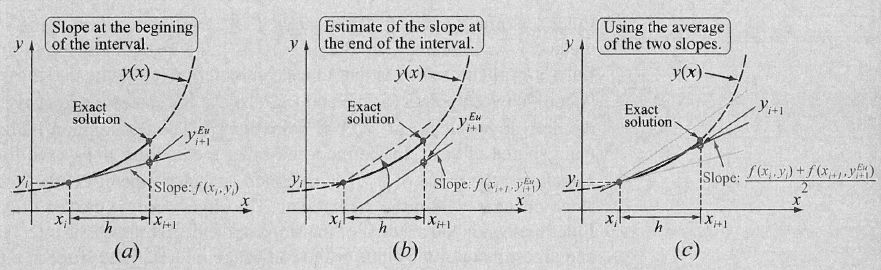
Beim modifizierten Verfahren wird zuerst die Steigung bei $(x_i, y_i)$ und bei $(x_{i+1}, y_{i+1})$ berechnet. Danach wird der nächste Punkt mit dem Mittel zwischen den beiden Steigungen den nächsten Punkt berechnet.

Fehler

Der lokaler Fehler ist definiert als: $$ \varphi(x_i, h) := y(x_{i+1}) - y_{i+1} $$ Wenn der lokaler Fehler folgendermassen schreiben kann, dann hat es die Konsistenzordnung $p$: $$ \varphi(x_i, h)\le C\cdot h^{p+1} $$ Ebenfalls gibt es ein globalen Fehler, welcher definiert ist als: $$ y(x_n)-y_n $$ Wenn der globalen Fehler folgendermassen schreiben kann, dann hat es folgende Konvergenzordnung $p$: $$ |y(x_n)-y_n| \le C\cdot h^p $$ Wie auch an den Formeln von der Konsistenzordnung und Konvergenzordnung zu sehen ist, hängt dieser Fehler von der Schrittweite $h$ ab.

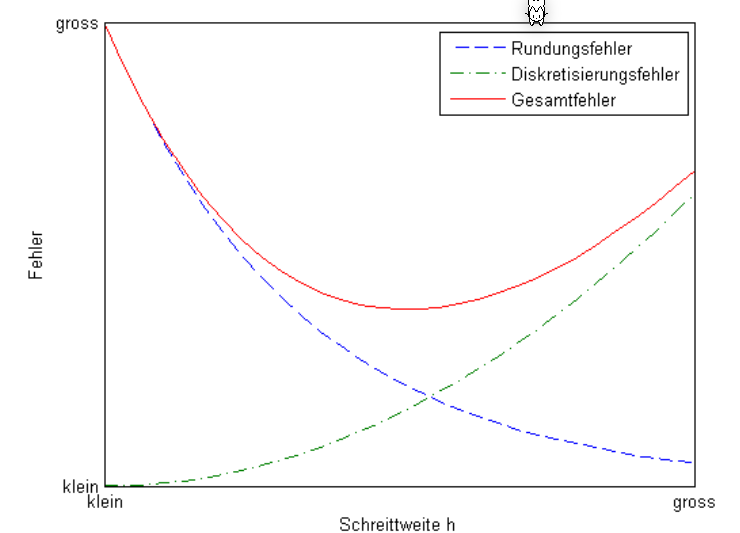
Es ist interesant ein Verfahren mit der Konvergenzordnung $p\ge 1$ und $h<1$, da dann $C\cdot h^p$ gegen $0$ strebt.

Für das Eulerverfahren gilt folgenden lokalen Fehler: $$ \begin{align} \varphi(x_n, h)=\frac{h^2}{2}y''(z) &&\text{, wobei } z \in [x_n, x_n+h] \end{align} $$ Das Mittelpunkt und modifizierte Eulerverfahren haben eine Konsistenz- und Konvergenzordnung $p=2$.

In der folgenden Abbildung ist der lokale Fehler für diverse Verfahren auf einem log-log Plot:

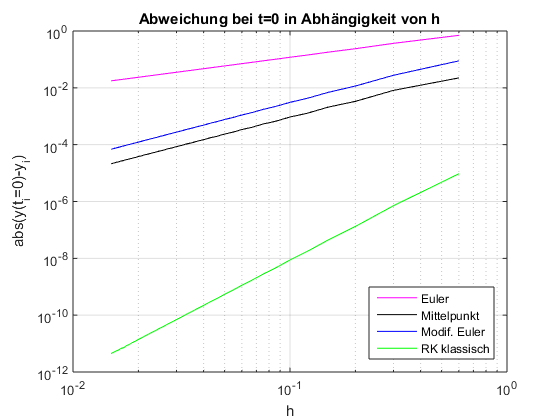
Runge-Kutta Verfahren

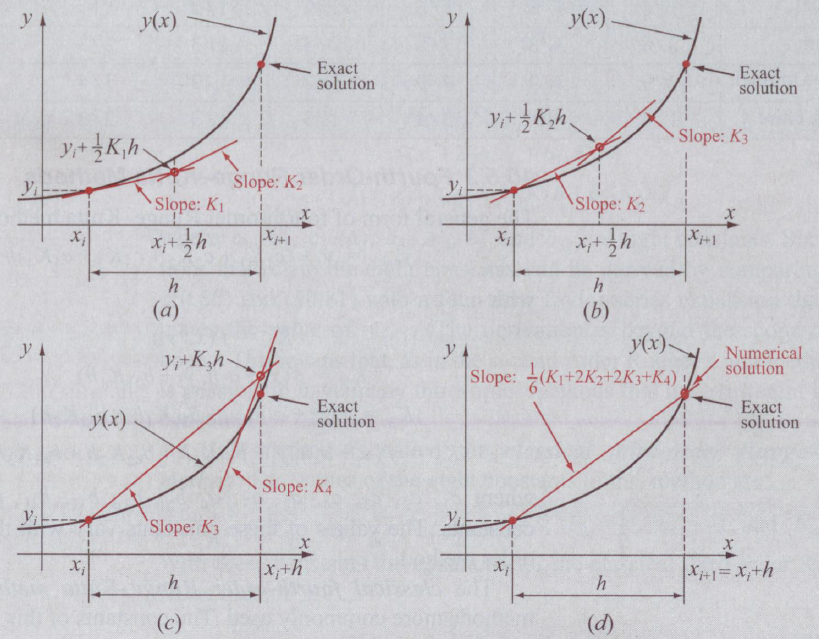
Im Runge-Kutta-Verfahren wird zuerst die Steigung $k_1$ bei $x_i$ berechnet, dann $k_2$ in der Mitte zwischen $x_i$ und $x_{i+1}$, $k_3$ ist ebenfalls beim Mittelpunkt, aber mit der Steigung $k_2$. Zuletzt wird $k_4$ am Punkt $x_{i+1}$ berechnet.

Die Konsistenz- und Konvergenzordnung von Runge-Kutta ist $p=4$.

Allgemeines s-stufiges Runge-Kutta-Verfahren

Das allgemeine s-stufige Runge-Kutta-Verfahren: $$ \begin{align} k_n&=f\left(x_i + c_nh, y+h \sum^{n-1}{m=1}a n=1,...,s\ y_{i+1}&=y_i+h\sum^s_{n=1}b_nk_n \end{align} $$ Dabei ist }k_m\right) && \text{für $s\in \N$ die Stufenzahl und $a_{nm}$, $b_n$ und $c_n$ sind Konstante.

Euler-Verfahren: $s=1$
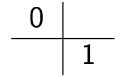
Mittelpunkt-Verfahren: $s=2$
Modifiziertes Euler-Verfahren: $s=2$
Klassisches Runge-Kutta Verfahren: $s=4$

Differentialgleichung-System

Um ein Differentialgleichung-System zu lösen, kann $y(x)$ als vektorwertige Funktion geschrieben werden.

Das Euler-Verfahren kann folgendermassen für Vektoren angepasst werden: $$ x_{i+1}=x_i + h\ \vec y_{i+1}=\vec y_i + \vec f(x_i, y_i)\cdot h $$ Oben ist es mit dem klassischen Eulerverfahren beschrieben. Dies kann aber mit allen Eulerverfahren gelöst werden.

Beispiel

Das folgende Beispiel kommt aus dem nächsten Unterkapitel "Differentialgleichung k-ter Ordnung zu DGL-System". $$ \begin{align} z_1'&=z_2\ z_2'&=z_3\ z_3'&=10e^{−x} − 5z_3 − 8z_2 − 6z_3 \end{align} $$ Zu dem gelten folgende Anfangswerte: $$ \vec z(0)=\begin{pmatrix}2 \ 0 \ 0\end{pmatrix} $$ Nun kommen die Iterationen:

Differentialgleichung k-ter Ordnung zu DGL-System

Um eine Differentialgleichung mit Ableitungen höher als erster Ableitungen zu lösen gibt es einen Trick: $$ y'''+5y''+ 8y' + 6y = 10e^{-x} $$

Nachh der höchsten Ableitung umformen: $y''' = 10e^{−x} − 5y'' − 8y' − 6y$
Alle Ableitungen von $y$ tiefer als die höchste Ableitungen durch $z_i$ ersetzen: $z_1=y, z_2=y', z_3=y''$
Und in der Gleichung einsetzen $y''' = 10e^{−x} − 5y'' − 8y' − 6y\Rightarrow z_3'=y''' = 10e^{−x} − 5z_3 − 8z_2 − 6z_3$
Es sind nun drei Gleichungen: $z_1'=y'=z_2$
$z_2'=y''=z_3$
$z_3' = 10e^{−x} − 5z_3 − 8z_2 − 6z_3$
In diesem Fall können sie auch vektoriel geschrieben werden: $\begin{pmatrix}z_2 \\ z_3 \\ 10e^{−x} − 5z_3 − 8z_2 − 6z_3 \end{pmatrix}=\begin{pmatrix}z_1' \\ z_2' \\ z_3'\end{pmatrix}$

Mit der Start-Bedingungen: $\vec z(0)=\begin{pmatrix}0 \\ 0 \\ 0\end{pmatrix}$

Stabilität

Wie stabil eine Lösung einer DGL ist hängt von dem benutzten Verfahren, der Schrittbreite und dem spezifischen Anfangsproblem ab.

Interpolation

Gegeben sind $n+1$ Stützpunkte/Wertpaare $(x_i, y_i)$, wobei $x_i \neq x_i$ für $i\neq j$ gelten muss. Gesucht ist nun eine stetige Funktion $g$ mit der Eigenschaft $g(x_i)=y_i$ für alle $i=0, ..., n$

Polynominterpolation

Wenn $n+1$ Stützpunkte gegen sind, kann das Polynom $P_n(x)=a_0 + a_1x + a_2+x^2 + ... + a_nx^n$

Wenn $x$ ein Vektor ist, kann auch eine Vandermonde-Matrix gebildet werden: $$ \begin{align} a_0 + a_1x_0 + a_2+x_0^2 + ... &+ a_nx_0^n\ a_0 + a_1x_1 + a_2+x_1^2 + ... &+ a_nx_1^n\ ...& \ a_0 + a_1x_n + a_2+x_n^2 + ... &+ a_nx_n^n\ \end{align} $$

\[ \begin{pmatrix} 1 & x_0 & x_0^2 & ... & x_0^n\\ 1 & x_1 & x_1^2 & ... & x_1^n\\ & & & ... \\ 1 & x_n & x_n^2 & ... & x_n^n\\ \end{pmatrix} \cdot \begin{pmatrix} a_0 \\ a_1 \\ ... \\ a_n\\ \end{pmatrix} = \begin{pmatrix} y_0 \\ y_1 \\ ... \\ y_n\\ \end{pmatrix} \]

Diese Rechnung ist allerdings oft schlecht Konditioniert und wird für $n> 20$ Stützpunkte instabil. Ein möglichen Ersatz ist das Lagrange Polynom

Lagrange Interpolation

Das Lagrange Polynom kann für $n$ Stützpunkte berechnet werden und ergibt ein Polynom mit dem Rang $n-1$. $$ P_n(x)=\sum^n_{i=0}I_i(x)y_i\ I_i(x)=\prod^n_{\substack{j=0\i\neq j}}\frac{x-x_j}{x_i-x_j} $$ Der maximale absoluten Fehler der dabei entstehen kann ist: $$ |f(x)-P_n(x)| \le \frac{|(x-x_0)(x-x_1)...(x-x_n)|}{(n+1)!}\cdot(\max_{x0\le \xi \le x_n}|f^{(x+1)}(\xi)|) $$ Als Bemerkung $f^{(x+1)}$ ist die $(x+1)$-te Ableitung

Da für die Fehlerberechnung die eigentliche Funktion $f$ benötigt wird, ist dies recht nutzlos.

Spline Interpolation

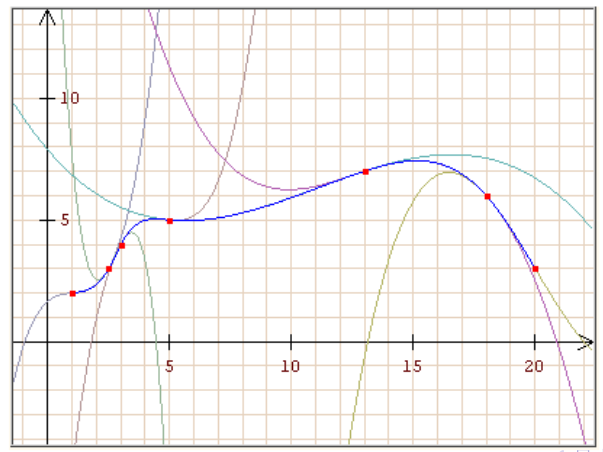
Es wird für jedes Intervall $[x_i, x_{i+1}]$ (für $i=0, 1, 2,, ..., n-1$) wird ein Polynom $s_i$ angesetzt. Das Polynom muss folgende Gleichungen erfüllen:

Es muss durch alle Punkte im Intervall $[x_i, x_{i+1}]$ gehen $s_i(x_i)=y, s_i(x_{i+1})=y_{i+1}, ...$
Der Übergang zwischen den Polynomen muss stetig sein $s_i(x_{i+1})=s_{i+1}(x_{i+1})$
Es darf kein Knick beinhalten $s_i'(x_{i+1})=s_{i+1}'(x_{i+1})$
Die Krümmung von zwei Splines soll auch gleich sein $s_i''(x_{i+1})=s_{i+1}''(x_{i+1})$

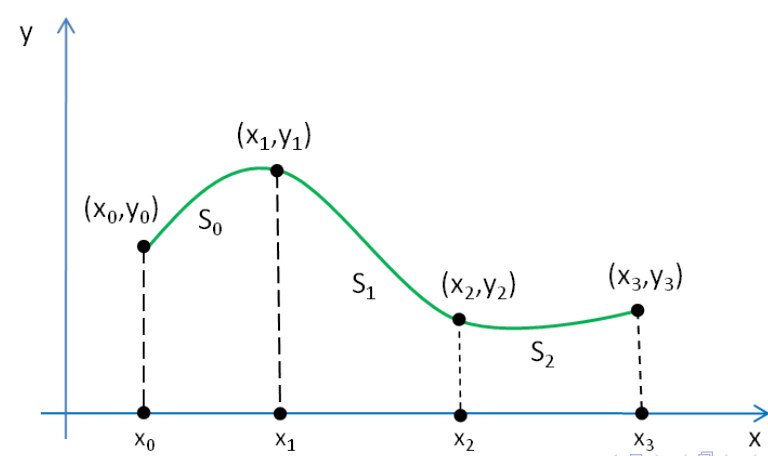
Um die Spline von oben zu berechnen, können nun folgende Polynome definiert werden: $$ \begin{align} S_0&=a_0+b_0(x-x_0)+c_0(x-x_0)^2 + d_0(x-x_0)^3 &, x\in [x_0, x_1] \ S_1&=a_1+b_1(x-x_1)+c_1(x-x_1)^2 + d_1(x-x_1)^3 &, x\in [x_1, x_2]\ S_2&=a_2+b_2(x-x_2)+c_2(x-x_2)^2 + d_2(x-x_2)^3 &, x\in [x_2, x_3]\ \end{align} $$ Aus diesen können nun folgendes Gleichungssytem aufgestellt werden: $$ \begin{align} S_0(x_0)&=y_0\ S_1(x_1)&=y_1 \ S_2(x_2)&=y_2 \ S_2(x_3)&=y_3 \ \ S_0(x_1)&=S_1(x_1)\ S_1(x_2)&=S_2(x_2)\ \ S_0'(x_1)&=S_1'(x_1)\ S_1'(x_2)&=S_2'(x_2)\ \ S_0''(x_1)&=S_1''(x_1)\ S_1'0(x_2)&=S_2''(x_2)\ \end{align} $$ Dies sind aber "nur" 10 Gleichungen, nicht die benötigten 12. Daher gibt es noch zusätzliche Bediungen:

natürliche kubische Splinefunktion $S_0''(x_0)=0, S_2(x_3)''=0$
peridodische kubische Splinefunktion $S_0'(x0)=S_2'(x_3), S_0''(x0)=S_2''(x_3)$
kubische Spliefunktion (mit not-a-knot Bedinungen) $S_0'''(x_1)=S_1'''(x_1), S_1'''(x_2)=S_2'''(x_2)$

Algorithmus

Für $n+1$ Stützpunkte werden $n$ Gleichungen nach der Form $S_i=a_i+b_i(x-x_i)+c_i(x-x_i)^2 + d_i(x-x_i)^3, x\in [x_i, x_{i+1}]$ gesucht. Dafür kann folgender Algorithmus für jedes $S_i$ angewendet werden:

Wenn die natürliche kubische Splinefunktion gesucht ist, wird $c$ auf $0$ gesetzt damit die zweite Ableitung $0$ ergibt $c_0=0, c_n=0$
Für jedes Polynom $S_i$
$a_i=y_i$
Die Breite des Intervalles $h_i=x_{i+1}-x_i$
$c_i$ bestimmen
$b_i$ und $d_i$ für jedes $S_i$ bestimmen
$b_i=\frac{y_{i+1}-y_i}{h_i}-\frac{h_i}{3}(c_{i+1}+2c_i)$
$d_i=\frac 1{3h_i}(c_{i+1}-c_i)$

Für das Beispiel $...$:

$i$	0	1	2	3
$x_i$	0	1	2	3
$y_i$	2	1	2	2
$a_i$	2	1	2	-
$h_i$	1	1	1	-
$c_i$	0	?	?	0

Um $c_1$ und $c_2$ zu finden kann folgendes Gleichungssystem gelöst werden: $$ A=\begin{pmatrix} 2(h_0+g_1) & h_1 \ h_1 & 2(h_1+h_2) \end{pmatrix} \ A \cdot \begin{pmatrix}c_1 \ c_2 \end{pmatrix} = \begin{pmatrix}

\end{pmatrix} $$

Lineare Ausgleichunsrechnung

Es wird eine Funktion gesucht, in der Form: $$ f(x)=\lambda_1f_1(x)+... + \lambda_mf_m(x) $$ Ein mögliches Beispiel wäre: $f(x)=\lambda_1 \cdot \underbrace{1}_{f_1(x)} + \lambda_2\cdot \underbrace x_{f_2(x)} + \lambda_3 \cdot \underbrace{x^2}_{f_3(x)}$

Um nun die $\lambda$s zu finden, damit $f(x)$ Datenpunkte nachgeht, muss der Fehler $E(f)$ zu den Datenpunkten minimieren:

$$ E(f)=w\cdot||y_f-(x)||2^2 = \sum^nw_i\cdot (y_i - f(x_i))^2 $$ Mit $w$ kann ein Punkt stärker oder schwächer gewichtet werden

Um dies zu minimieren, wird die Ableitung von $E(f)=0$ gesetzt:

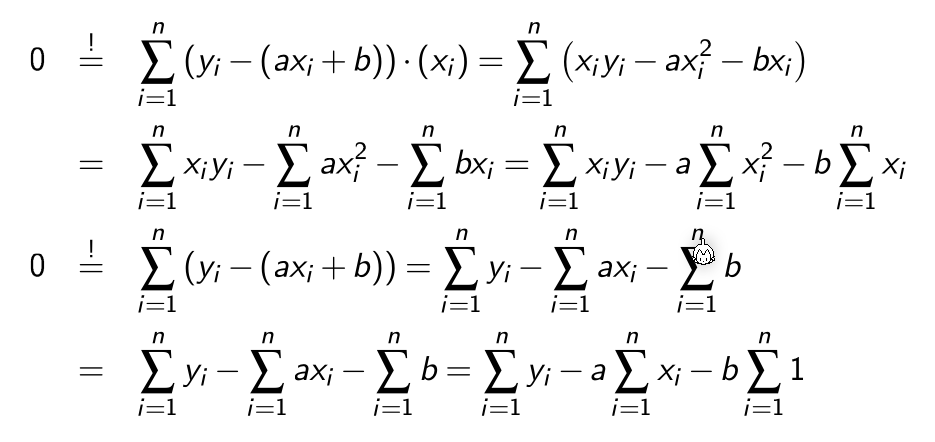
Aus dem folgt:

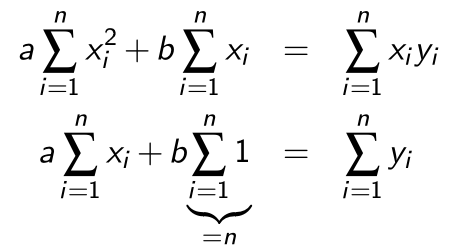
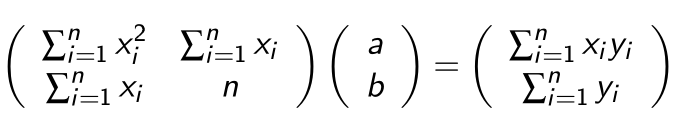
Dies funktioniert allerdings nur für eine Gerade. Die selbe Methode kann aber auch für höhere Polynomen verwendet werden: $$ E(f)=||\vec y-f(\vec x)||2^2=\sum^n\lambda_jf_j(x_i)\right)^2=||\vec y-A\lambda||_2^2 $$ Mit folgender Matrix }(y_i-f(x_i))^2 = \sum^n_{i=1}\left(y_i - \sum^m_{j=1$A$:

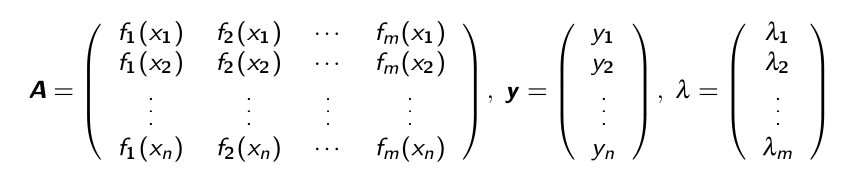
Die Gleichung $E(f)=0$ hat nur im Spezialfall eine Lösung, wenn $m=n$ und wenn die Funktion $f$ durch alle Punkte geht.

Normalgleichungen

Um $E(f)$ zu minimieren muss die erste Ableitung von $E'(f)=0$ sein. Daher muss $E(f)$ nach jedem $\lambda$ abgeleitet werden: $$ \frac{\part E(f)(\lambda_1, ..., \lambda_m)}{\part \lambda_j}=0 , j=0,...,m $$ Dies nennt sich eine Normalgleichung und lässt sich als $A^TA\lambda=A^Ty$.

$A$ ist oft schlecht konditioniert und die Lösung sollte daher mit dem QR-Verfahren gelöst werden.

Linearisieren

Falls eine $f$ Funktion auf den ersten Blick nicht linear erscheint, kann sie eventuell linearisiert werden.

Z.B. die Funktion $ae^{bx}$ kann mit $\log_e$ linearisiert werden.

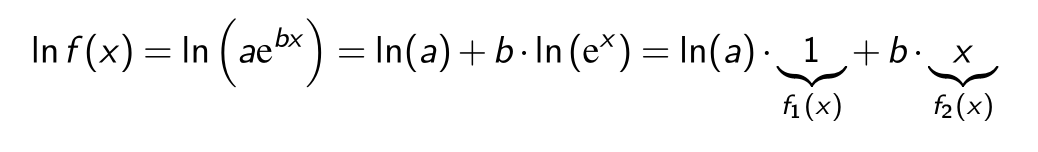
Nicht-Lineare Ausgleichsrechnung

\[ f(\lambda_1, \lambda_2, ..., \lambda_m, x)=... \]

Das allgemeine Ausgleichsproblem besteht darin folgendes $E$ zu minimieren:

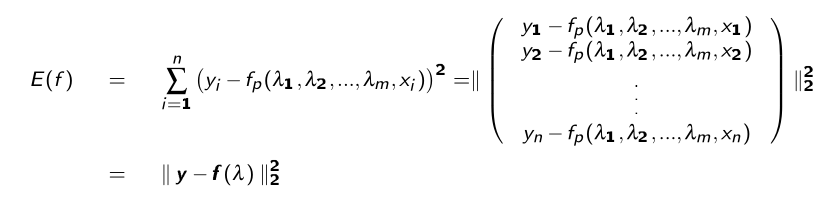
Die Ableitung von $E$ wird auf $E'(f)=0$ gesetzt. Dafür kann das Gauss-Newton-Verfahren.

Gauss-Newton-Verfahren

Das Quadratmittelproblem ist es einen Vektor $x\in\R^m$ zu finden, welcher die Fehlerfunktional $E: \R^m \to \R:=||g(x)||_2^2$ minimiert. $E$ gehört zur Funktion $g: \R^m \to \R^n$

$g$ wird nun definiert als $g(\lambda):=y-f(\lambda)$.

Um nun für eine nicht lineare Funktionen $f$ eine Lösung zu finden, muss $f$ linearisiert werden: $$ \begin{align} g(\lambda)&\approx g(\lambda_0)+Dg(\lambda_0)\cdot(\lambda - \lambda_0)\ \ Dg(x)&=\begin{pmatrix} \frac{\partial g_1}{\partial x_1}(\vec x) & \frac{\partial g_1}{\partial x_2}(\vec x) & ... & \frac{\partial g_1}{\partial x_n}(\vec x) \

\frac{\partial g_2}{\partial x_1}(\vec x) & \frac{\partial g_2}{\partial x_2}(\vec x) & ... & \frac{\partial g_2}{\partial x_n}(\vec x) \

... & ... & ... & ... \ \frac{\partial g_m}{\partial x_1}(\vec x) & \frac{\partial g_m}{\partial x_2}(\vec x) & ... & \frac{\partial g_m}{\partial x_n}(\vec x) \ \end{pmatrix} \end{align} $$ $E$ kann nun folgendermassen definiert werden: $$ \tilde E(\lambda) = ||\underbrace{g(\lambda_k)}{\tilde y} + \underbrace{Dg(\lambda_k)}_\delta||_2^2 $$ Wobei } \cdot \underbrace{(\lambda-\lambda_k)$k=0,1,...$ ist.

Dies kann nun wie eine lineare Gleichung gelöst werden: $$ Dg(\lambda_k)^TDg(\lambda_k)\delta_k=-Dg(\lambda_k)^T\cdot g(\lambda_k) $$ Oder mit dem QR-Verfahren: $$ Dg(\lambda_k)=Q_kR_k\ R_k\lambda_k=-Q_k^Tg(\lambda_k) $$ Für jedes $k$ wird nun $\tilde E$ minimiert, bzw. die obere Gleichung aufgelöst.

Das nächste $\lambda$ kann wie folgt ausgerechnet wird: $$ \lambda_{k+1}=\lambda_k+\delta_k $$

Gedämpftes Gauss-Newton-Verfahren

Das gedämpte Gauss-Netwon-Verfahren funktioniert gleich, wie das "normale" Verfahren, nur das $\delta_k$ verkleinert wird.

Um das $\delta_k$ für die nächste Iteration zu finden, soll folgende für folgende Formel das minimale $p\in{0, 1, ..., p_{max}}$ gefunden werden $$ ||g\left(\lambda_k+\frac{\delta_k}{2^p}\right)||2^2 < ||g(\lambda_k)||_2^2 $$ $\lambda_{k+1}$ wird nun folgendermassen berechnet: $$ \lambda $$ Falls kein minimales }=\lambda_k+\frac{\delta_k}{2^p$p$ gefunden werden kann, wird mit $p=0$ gerechnet.

Nichtlineare Gleichungssysteme

Multivariate Funktionen

Skalarwertige Funktion

Eine Funktion, welche mehrere $x$-Werte nimmt und ein $y$-Wert zurück gibt. $$ f: \mathbb R ^n \to \mathbb R \ y = f(x_1, x_2, ..., x_n) $$

Vektorwertige Funktion

Eine Funktion, welche mehrere $x$-Werte nimmt und mehrere $y$-Werte zurück gegeben $$ f: \mathbb R^n \to \mathbb R^m \ (y_1, y_2, ..., y_m) = f(x_1, x_2, ..., x_n) $$

Explizite und implizite Funktionen

Explizite Funktionen haben die folgende Form: $y=f(x_1, x_2, ..., x_n)$

Implizite Funktionen haben die folgende Form: $F(x_1, x_2, ..., x_n, y)=0$

Partielle Ableitung

Um die Funktion $z=f(x, y) = 2x^2 + 5 y$ abzuleiten, kann nach $x$ und $y$ separat abgeleitet werden: $$ \begin{align} \text{nach }x: \frac{\partial f}{\partial x} &= 4x + 0 \ \text{nach }y: \frac{\partial f}{\partial y} &= 0 + 5 \ \end{align} $$ Diese Ableitung kann folgendermassen visualisiert werden:

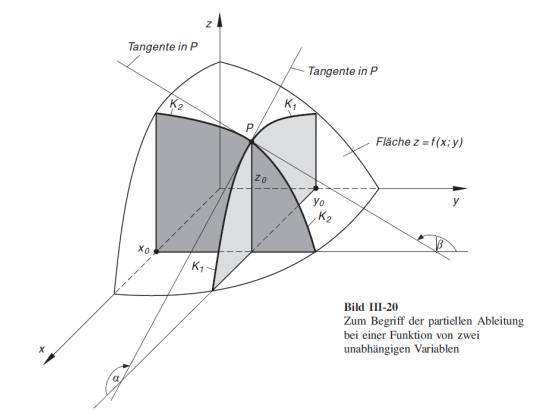
Jacobi-Matrix

Für die Funktion $f: \mathbb R^n \to \mathbb R^m$ mit $\vec y = f(\vec x)=\begin{pmatrix}y_1=f_1(\vec x) \\ y_2 = f_2(\vec x)\\ ... \\ y_m=f_m(\vec x)\end{pmatrix}$ und $\vec x = (x_1, x_2, ..., x_n)^T$ ist die Jacobi-Matrix das folgende: $$ Df(x)=\begin{pmatrix} \frac{\partial f_1}{\partial x_1}(\vec x) & \frac{\partial f_1}{\partial x_2}(\vec x) & ... & \frac{\partial f_1}{\partial x_n}(\vec x) \

\frac{\partial f_2}{\partial x_1}(\vec x) & \frac{\partial f_2}{\partial x_2}(\vec x) & ... & \frac{\partial f_2}{\partial x_n}(\vec x) \

... & ... & ... & ... \ \frac{\partial f_m}{\partial x_1}(\vec x) & \frac{\partial f_m}{\partial x_2}(\vec x) & ... & \frac{\partial f_m}{\partial x_n}(\vec x) \ \end{pmatrix} $$ In dieser Matrix ist in einer Reihe alle möglichen partiellen Ableitungen für $f_1(\vec x)$

Linearisierung

Eine Approximation für $y=f(x)$ kann mit $f(x)\approx f(x_0) + f'(x-x_0)$.

Dasselbe kann auch für eine multivariante Funktion mithilfe der Jacobi-Matrix getan werden: $g(\vec x)=f(\vec {x_0}) + Df(\vec {x_0})\cdot (\vec x-\vec {x_0})$

($Df(\vec x)$ ist die Jacobi-Matrix)

Nach dem Linearisieren wird ein nichtlineare Funktion lineare und kann mit bekannten Verfahren gelöst werde

Newton-Verfahre

Das Newton-Verfahren erwartet, dass $f(\vec x_n)=\vec 0$ gilt.

\[ \vec x_{n+1}=\vec x_n-(Df(\vec x_n))^{-1}\cdot f(\vec x_n) \]

Um nicht die Jacobi-Matrix invertieren zu müssen, kann folgender Trick angewendet werden: $$ \vec \delta_n :=-(Df(\vec x_n))^{-1}\cdot f(\vec x_n)\ \text{Dies kann in folgendes Umgewandlet werden:}\ Df(\vec x_n)\cdot \vec\delta x_n = -f(\vec x_n) $$ Die Gleichung $Df(\vec x_n)\cdot \vec\delta x_n = -f(\vec x_n)$ ist ein lineares Gleichungssystem, welches relativ einfach gelöst werden kann. Danach kann $\vec \delta _n$ anstelle von $-(Df(\vec x_n))^{-1}\cdot f(\vec x_n)$ verwendet werden: $\vec x_{n+1}=\vec x_n+\vec \delta_n$

Das Newton-Verfahren konvergiert quadratisch für nah genug an einer Nullstelle $\overline x$ liegende Startwerte, wenn $Df(\overline x)$ regulär und $f$ dreimal stetig differenzierbar ist.

Für eine Nichtreguläre Matrix A gilt $\det(A)\ne 0$

Mögliche Abbruchskriterien sind:

$n > n_{max}$
$||\vec x_{n+1}-\vec x_n||\le ||\vec x_{n+1}||\cdot \varepsilon$
$||\vec x_{n+1}-\vec x_n||\le \varepsilon$
$||f(\vec x_{n+1})||\le \varepsilon$$

Vereinfachtes Newton-Verfahren

Beim regulären Newton-Verfahren muss bei jeden Iterationsschritt die Jacobi-Matrix $Df(\vec x)$ neuberechnen. Beim vereinfachten Newton-Verfahren wird $Df(\vec x)$ nur für den Startvektor berechnet. $$ \vec x_{n+1}=\vec x_n-(Df(\vec x_0))^{-1}\cdot f(\vec x_n)\ Df(\vec x_0)\cdot \vec\delta x_n = -f(\vec x_n) $$ Wegen dieser Vereinfachung kovergiert das Verfahren nur noch linear gegen die Nullstelle, wenn $Df(\overline x)$ nicht regulär ist.

Gedämptes Newton-Verfahren

Wenn $Df(\vec x_n)$ schlecht konvergiert, dann kann nicht generell erwartet werden, dass $\vec x_{n+1}=\vec x_n + \vec \delta_n$ nicht gilt.

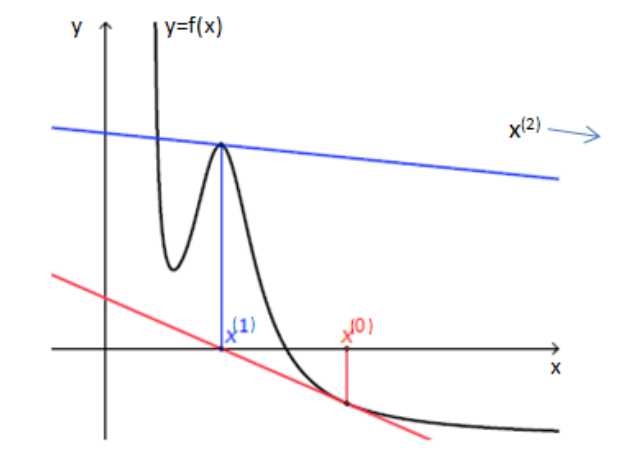
Für das gedämpfte Newton-Verfahren werden folgende Schritte angewendet:

Berechne $\delta_n$ mit $Df(\vec x_n)\delta_n=-f(\vec x_n)$ ausgerechnet
Finde das minimale $k\in \{0, 1, ...\}$ für das gilt: $||f(\vec x_n + \frac{\vec \delta_n}{2^k})||_2 < ||f(\vec x_n)||_2$
Wenn kein $k$ gefunden wird, soll mit $k=0$ weiter gerechnet werden
Nun soll die Iterationsgleichung $\vec x_{n+1}=\vec x_n + \frac{\vec \delta_n}{2^k}$ verwendet werden# Numerische Itegration

Rechteck- & Trapezregel

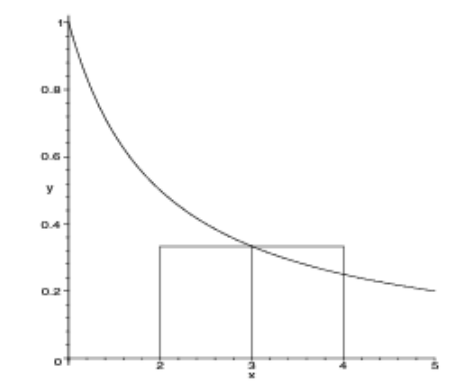
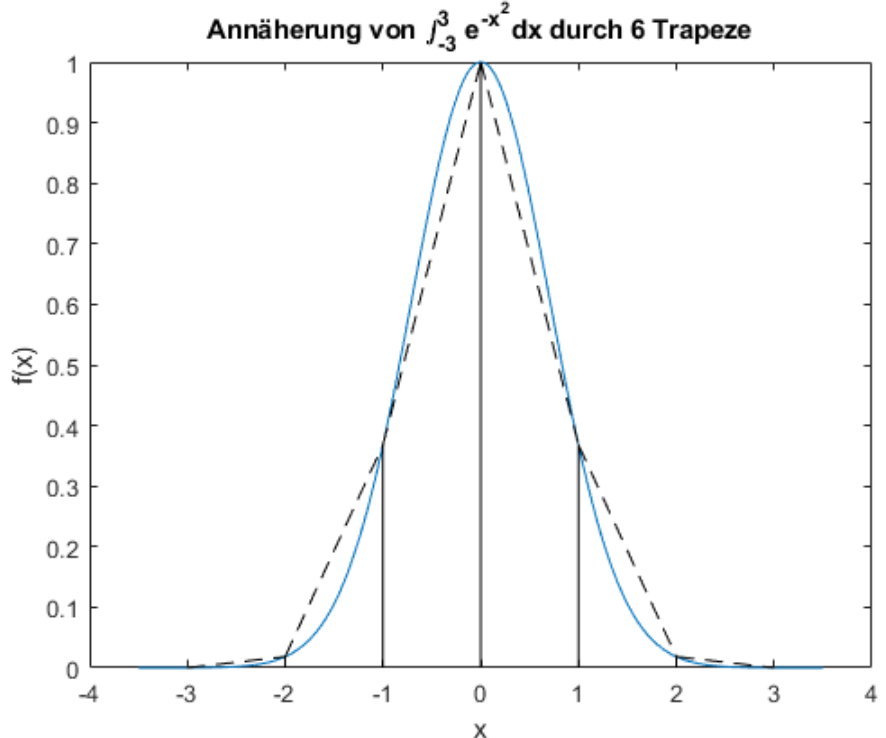
Die folgenden formel ziehen ein Rechteck, bzw. Trapez über das ganze Integral. $$ \text{Das Integral}\ \int_a^b f(x)\mathrm d x\ \ \text{kann folgendermassen approximiert werden}\ Rf=f\left(\frac{a+b}{2}\right) \cdot (b - a)\ Tf=\frac{f(a) + f(b)} 2 \cdot (b - a) $$ (Rf = Rechtecksregel, Tf = Trapezregel)

Für die summierte Rechteck- & Trapezregel wird das Integral in kleinere Schritte mit der breite $h$ unterteilt. $$ Rf(h)=h\cdot \sum^{n-1}{i=0} f(x_i +\frac h 2)\ Tf(h)=h\cdot \left(\frac{f(a) + f(b)}{2} +\sum^{n-1} f(x_i) \right)\ \text{wobei gilt} x_i=a+i\cdot h\ h=\frac{b-a} n $$

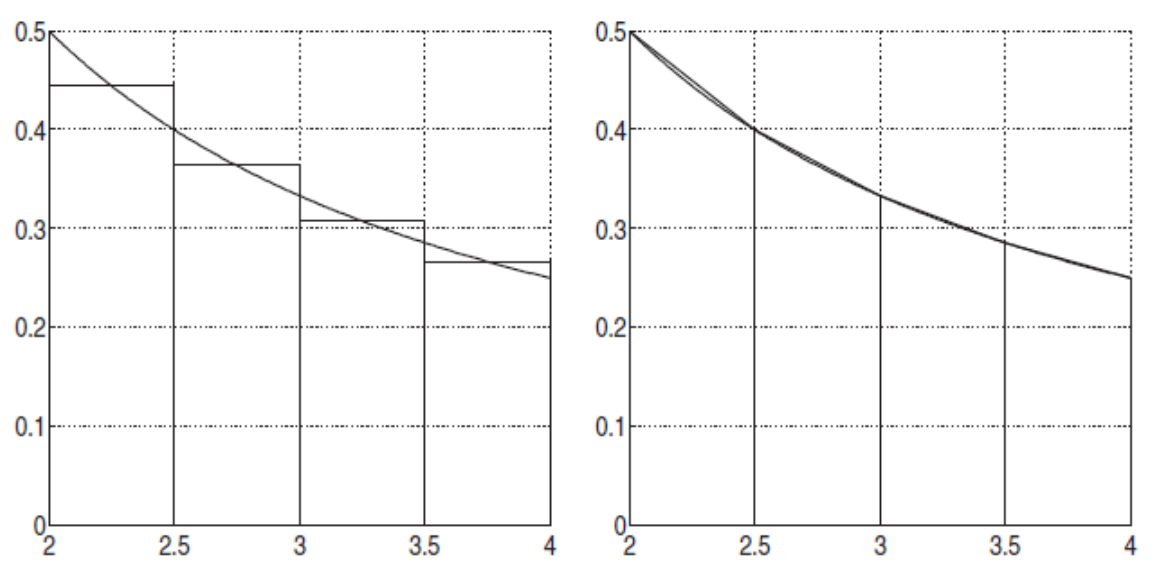
Simpsonregel

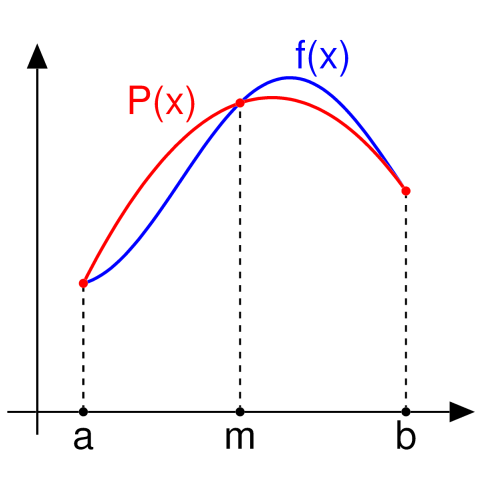
Für das lösen eines Segments müssen folgende Formel ausgerechnet werden. Dabei wird das Polynom $p(x)=\alpha+\beta(x-a) + \gamma(x-a)(x-b)$ verwendet.

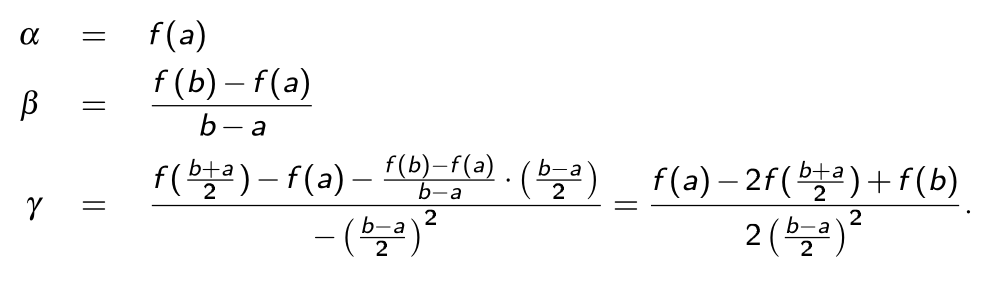
Da $f(x)\approx p(x)$ gilt, kann das Polynom integriert werden:

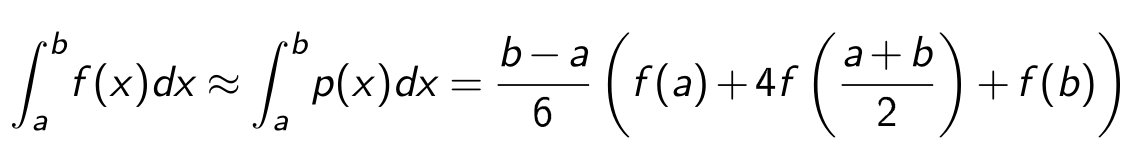
Die Regel oben haben nur ein Segment benutzt. Wie aber auch bei der Rechtecks- und Trapezregel, kann auch hier die summierte Simpsonregel verwendet werden. $$ Sf(h)=\frac h 3 \left(\frac 1 2 f(a) + \sum^{n-1}{i=1} f(x_i) + 2 \sum^n \right) + \frac 1 2 f(b) \right) $$ Die Simpsonsregel kann auch mit dem Rechtecks- und Trapezregel berechnet werden: $$ Sf(h)=\frac 1 3 (Tf(h) + 2 Rf(h)) $$} f\left (\frac{x_{i-1}+x_i}{2

Fehlerabschätzung

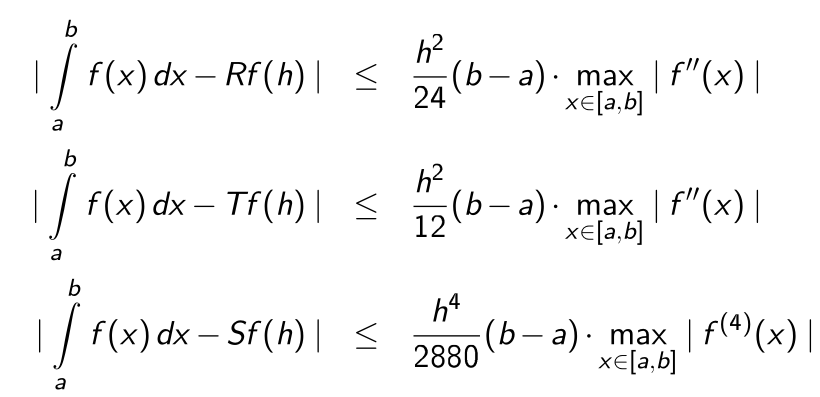
Gaussformel

Die folgenden Formel bestimmen das Integral zwischen $a$ und $b$, wenn es $n$ Stützpunkte gibt. Dabei müssen die Stützpunkte nicht äquidistant sein.

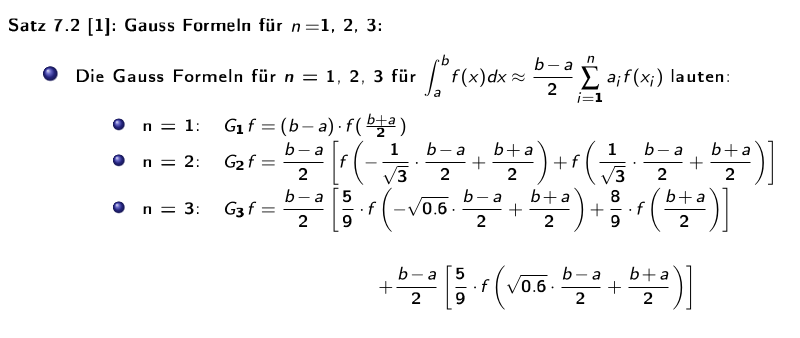
Romberg Extrapolation

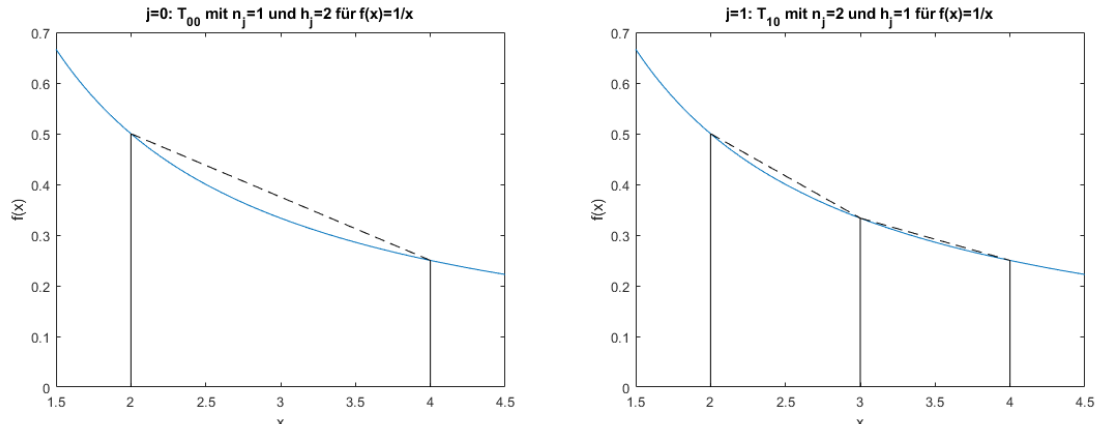
Die Rekursion wird ausgerechnet bis $k=0$ wird, da dann die Formel $T_{j0}=Tf\left(\frac{b-a}{2^j}\right)$

Da die Werte von $f(...)$ immer in $T_{j0}$ wiederverwendet werden, kann dies mit der folgenden Formel vereinfacht werden: $$ T_{j0}=\frac 1 2 T_{j-1,0}+h_j\sum^{n_{j-1}}_{i=1}f(a+(2i-1)h_j) $$ Die zweite Spalte $T_{j1}$ kann mit der Simpson-Regel berechnet werden: $$

$$

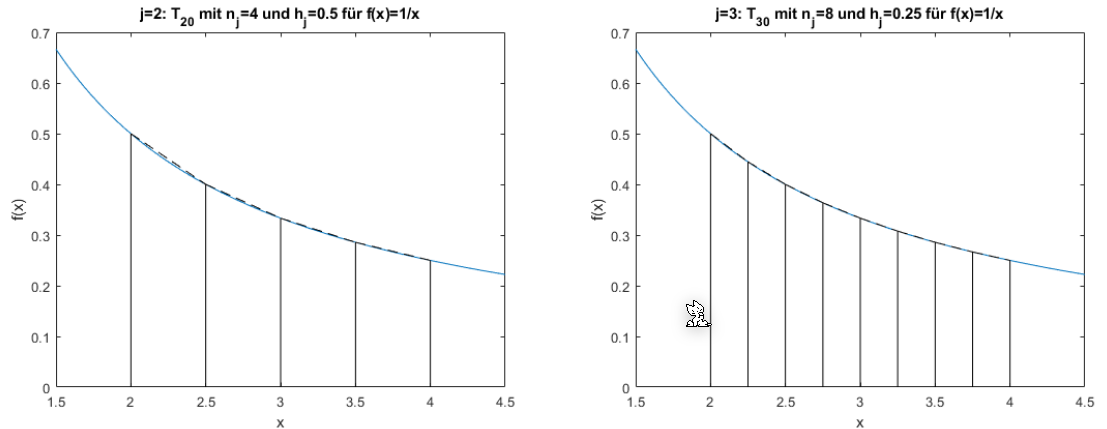
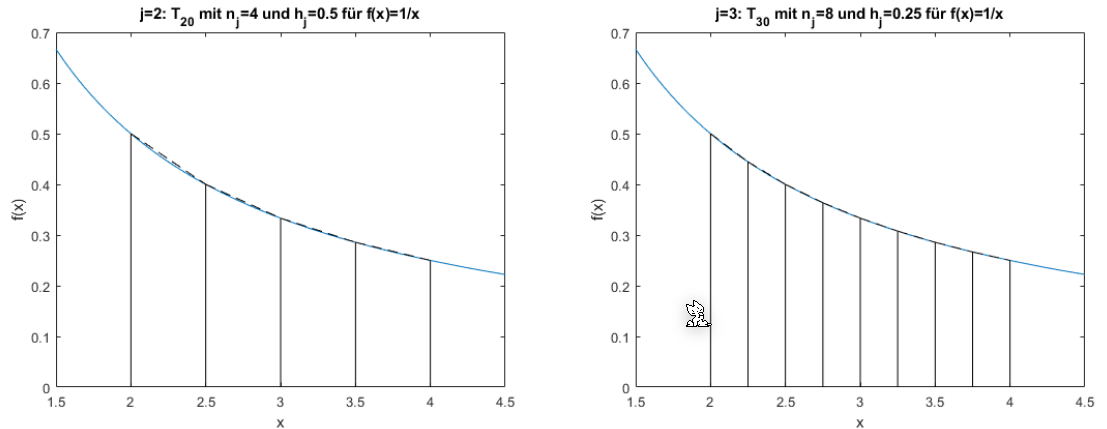
Die folgende Graphik zeigt die oben abgebildete Rekursion:

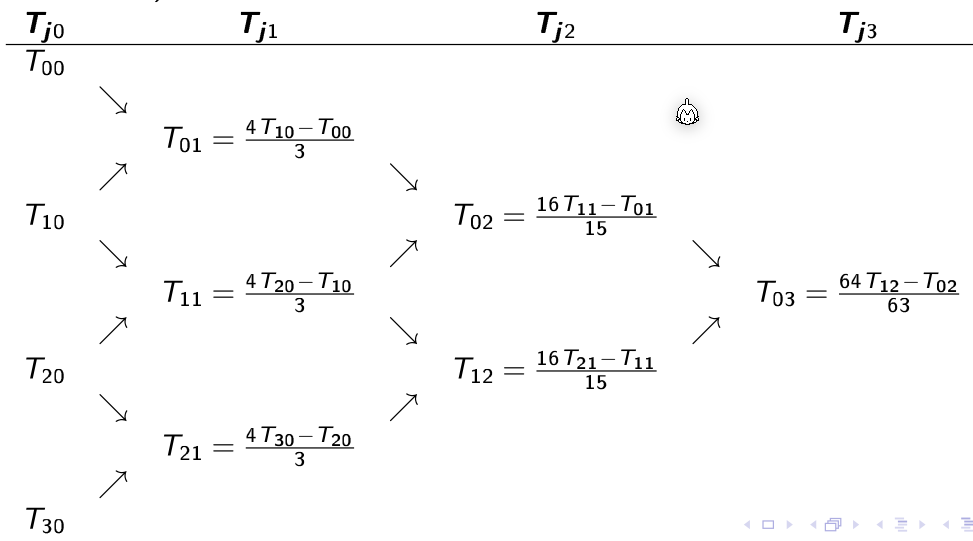
Die folgenden zwei Graphen zeigen $T_{00}$ und $T_{10}$. Wenn $j$ um 1 höher wird, wird die X-Achse halbiert. Dasselbe gilt für $T_{30}$ und $T_{40}$

\(i\)	0	1	2	3
\(x_i\)	0	1	2	3
\(y_i\)	2	1	2	2
\(a_i\)	2	1	2	-
\(h_i\)	1	1	1	-
\(c_i\)	0	?	?	0