Definitionen

Alphabet

Ein Alphabet ist ein endliche, nichtleere Menge von Symbolen.

Als Beispiel: $\Sigma=\{a, b, c\}$ $\N$ wäre kein Alphabet, das es nicht endlich ist!

Wörter

Ein Wort ist eine endliche Folge von Symbolen eines bestimmten Alphabets.

Das leere Wort $\varepsilon$ ist ein Wort, welches keine Symbole enthaltet. Dieses Wort gibt es über jedem Alphabet.

Als Beispiel: $abc$ ist ein Wort über dem Alphabet $\Sigma_{lat}$. Wörter können auch als Mengenschreibweisse dargestellt werden.

Länge eines Wortes

Der Betrag eines Wortes ist die Länge des Wortes.

Beispiel:

$|abc|=3$
$|\varepsilon|=0$

Absolute Häufigkeit

$|w|_x bezeichnet die absolute H$uffigkeit eines Symboles $x$ in einem Wort $w$

Beispiel:

$|abc|_a=1$
$|100111|_1=4$
$|\varepsilon|_{\varepsilon}=1$

Spiegelwort

Mit $w^R$ wird das Spiegelwort zu $w$ bezeichnet. $$ W^R=(x_1, x_2...x_n)^R=(x_n...x_2,x_1) $$ Dabei gilt, dass $|w|=|w^R|$ und $|w|_x=|w^R|_x$

Wenn $w=w^R$ gilt, dann wird $w$ als Palindrom bezeichnet

Beispiel:

$(abc)^R=cba$

Teile von Wörter

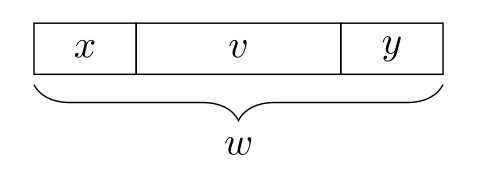
Der start eines Wortes $w$ wird Präfix genannt. Symbole in der Mitte werden Infixe oder auch Teilwörter. Das Ende eines Wortes $w$ wird Suffix genannt.

Ein Präfix, Infix oder Suffix ist echt, wenn sie nicht gleich das Wort $w$ ist

Menge aller Wörter mit einer Länge

Die Menge aller Wörter der Länge $k$ über einem Alphabet $\Sigma$ wird mit $\Sigma^k$ bezeichnet.

$\Sigma^0=\{\varepsilon\}$ Dies ist per Definition für alle Alphabete gegeben.

Beispiel: $\{0, 1\}^2=\{00, 01, 10, 11\}$

Kleenesche Hülle

Die Menge aller Wörter $\Sigma^*$ in einem Alphabet wird Kleenesche Hülle genannt und ist abzählbar Unendlich

$\Sigma^+=\Sigma^*\setminus\{\varepsilon\}$ und ist die Menge aller Wörter über $\Sigma$ ohne das leere Wort

Konkatination

$x\circ y=xy$ heisst, dass die Wörter $x$ und $y$ zusammen verkettet werden. Die Wörter müssen nicht aus demselben Alphabet kommen.

Es gilt zudem: $|x|+|y|=|xy|=|x\circ y|$

Beispiel: $x=22$ und $y=100$, dann gilt: $xy=x\circ y=22100$

Wortpotenzen

Die Wortpotenz ist definiert mit der folgenden Defintion $$ x^0=\varepsilon\ x^{n+1}=x^n\circ x $$

Beispiel:

$a^3=a^2a=a^1aa=a^0aaa=aaa$
$bbababababaaa=b^2(ab)^4a^3$ (Dies ist nicht die einzige Lösung)

Sprachen

Eine Teilmenge von Wörtern nennt man eine Sprache (Dies kann auch als $L\subseteq \Sigma^*$ geschrieben werden)

$\Sigma*$ ist auch eine Sprache über dem Alphabet $\Sigma$

Wenn $\Sigma_1 \subseteq \Sigma_2$ und $L$ eine Sprache über $\Sigma_1$ ist, dann ist $L$ auch eine Sprache über $\Sigma_2$

$\emptyset$ ist eine leere Sprache; Also eine Sprache ohne Wörter und gilt für jedes Alphabet ($\empty\neq \{\varepsilon\}$)

Sprache können aus unendlich vielen Wörtern bestehen. Die Wörter müssen aus einem endlichen Alphabet gebildet werden und müssen endlich lang sein.

Darstellungsmöglichkeiten:

$L=\{\varepsilon, 10, 1100, 111000, ...\}$
in Prosa
$L=\{1^n0^n|n\in \N\}$

Sprachen-Konkatenation

$A\subset \Sigma^*$ und $B\subset \Gamma^*$ sind zwei Sprachen, dann ist $AB=\{uv|u\in A \text{ und } v \in B\}$

Zudem gilt: Ist $A$ eine Sprache über $\Sigma$ und $B$ eine Sprache über $\Gamma$, dann ist $AB$ eine Sprache über dem Alphabet $\Sigma \cup\Gamma$

Kleenesche Hülle einer Sprache

Die Kleenesche Hülle $A*$ einer Sprache $A$ ist durch ${\varepsilon}\cup A \cup AA \cup AAA \cup ...$

Die Kleenische Hèlle einer Sprache ist selbst eine Liste von Wörter, da die Liste aber unendlich ist, ist sie selbst keine Sprache (stimmt das?)

Komplement einer Sprache

Das Komplement einer Sprache sind alle Wörter, welche nicht in der Sprache sind

$\overline L=\Sigma^*-L=\Sigma^*\setminus L$

Entscheidungsproblem

Sei eine Sprache $L$ über einem Alphabet $\Sigma$ gegeben. Das Entscheidungsproblem $(\Sigma, L)$ ist die folgende:

Input: Eine Sprache $L$ und ein Wort $x\in\Sigma^*$ Output: JA, falls $x\in L$ ist und NEIN, falls $x\not \in L$ ist

In Deutsch: "Gehört ein Wort eines Alphabetes zu einer Sprache?"

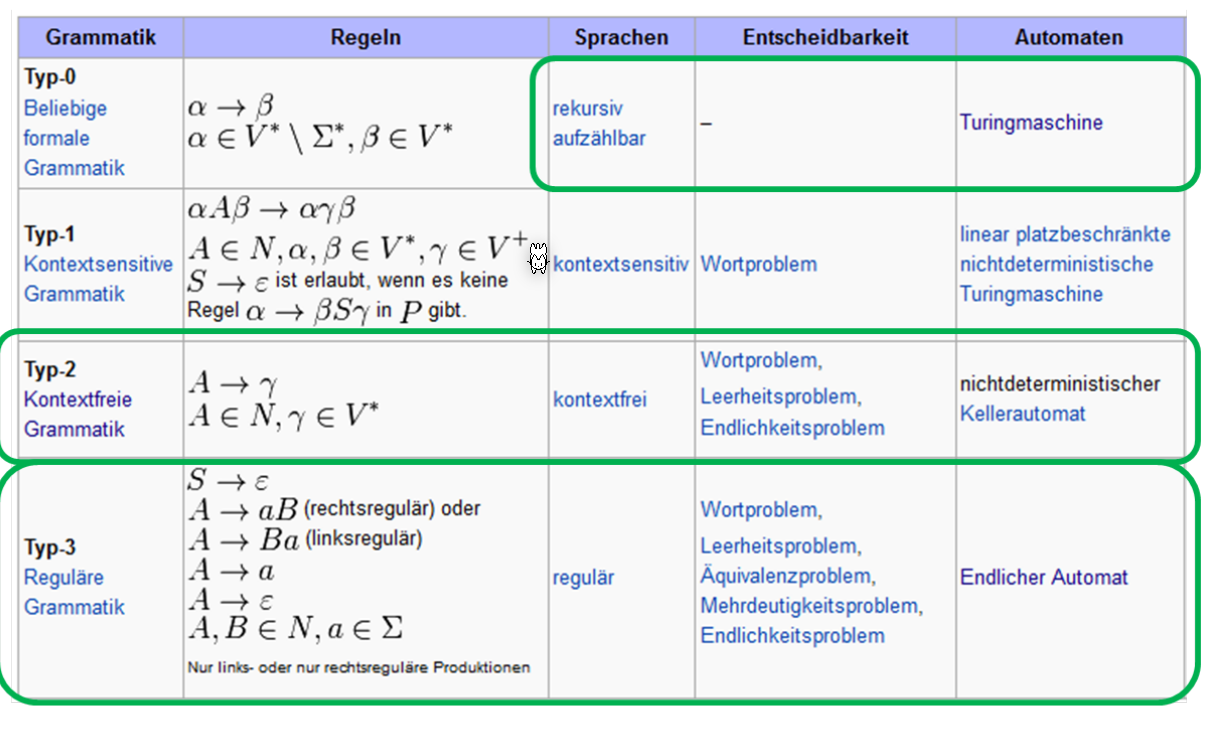
Chomsky-Hirarchie

Fragen

Ist die Kleenische Hülle einer Sprache wieder eine Sprache? - Ja