Was ist Information

Etwas, was das eigene Wissen erweitert; etwas neues, was wir vorhin noch nicht wussten
mit \(F=ceiling(log(_2(N))\)

Daten Quellen

Discrete Memoryless Source (DMS)

Discrete = Einzelne Nachrichten
Die einzelnen Nachrichten sind Unabhängig

Beispiele:

Würfel (errinnert sich nicht an den letzten Wurf, getrennte Nachrichten)
Liste von Nummerschild von Autos von einer Kamera auf der Autobahn

Binary Memoryless Source (BMS)

Wie eine DMS, aber nur 1 oder 0
(scheint ein wenig nutzlos zu sein…)

Irrelevanz

Informationen ist irrelevant, wenn für den Empfänger die Informationen nicht benötigt. Um dies festzustellen zu können, muss man wissen, für was der Empfänger die Informationen verwendet.

Mathe dahinter

Information

\(I(x)=log_2(\frac 1 {P(x)})\)

Diese Formel stellt dar, wie gross der Überraschungseffekt ist. Die Einheit ist "Bits".

(\(P(x)\) ist, wie wahrscheinlich es ist, dass x vorkommt)

Entropie

Die Entropie ist der gewichtete Durchschnitt der Informationen und wird mit folgender Formel berechnet:

\(H(X)=\sum^{N-1}_{n=0} P(x_n)\cdot I(x_n)=\sum^{N-1}_{n=0}P(x_n)\cdot log_2(\frac 1 {P(x_n)})\)

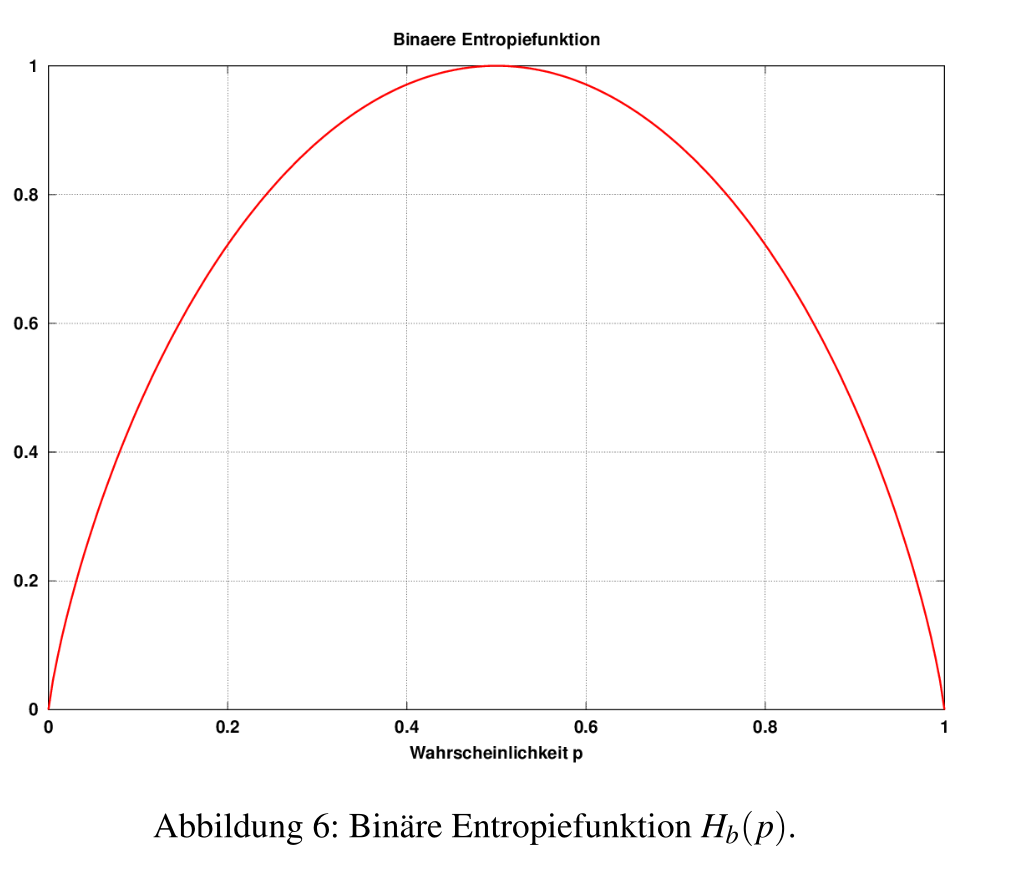
Das folgende Bild zeigt die Entropie von einer BMS mit der Wahrscheinlichkeit von \(p\) für das eine Zeichen (und die Wahrscheinlichkeit \(1-p\) für das andere Zeichen). Wie man sieht, ist die Entropie am höchsten, wenn alle Zeichen gleich oft Vorkommen.

Zweier Logarithmus ohne zweier Logarithmus

\(2^x=K\)
\(log(2^x)=log(K)\)
\(x\cdot log(2)=log(K)\)
\(x=\frac{log(K)}{log(2)}\)

Quellenkodierung

Redundanz

Daten, welche reversible entfernt werden können.

Um dies zu berechnen, kann man von der Code-Länge die Entropie abziehen. Jetzt kann es aber sein, dass es Codierungen gibt, bei welcher nicht alle Zeichen dieselbe Länge haben. Daher braucht man die mittlere Codewortlänge, welche wie folgt berechnet wird:

\(L(X)=\sum^{N-1}_{n=0}P(x_n)\cdot l(x_n)\)

(Also eigentlich einfach nur der gewichtete Durchschnitt von allen Codelängen)

Die Redundanz ist nun folgendes:

\(R(X)=L(X)-H(X)\)

Wenn die Redundanz < 0 ist, dann komprimiert man mit Verlüste, da nicht alle Informationen hineinpassen und somit Informationen weggeworfen wird

Huffman Codes

Codes mit dem Huffmanverfahren sind:

automatisch präfixfrei
optimal (Das heisst, es gibt keine besseren präfixfreie Code)

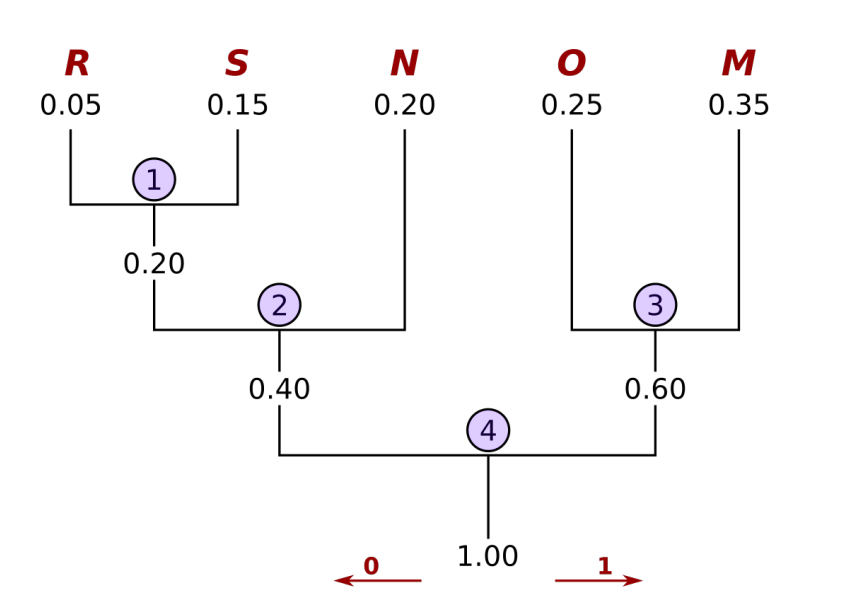
Vorgehen

Ordne alle Symbole nach aufsteigenen Auftretenswahrscheinlichkeiten auf einer Zeile. Dies sind die Blätter
Notiere unter jedes Blatt seine Wahrscheinlichkeit
Schliesse die beiden Blätter mit der kleinsten Wahrscheinlichekit an einer gemeinsamen Astgabel an und ordne dem Ast die Summe der Wahrscheinlichkeiten zu
Wiederhole Schritt 2 es nur noch ein Stamm gibt
Jedem Ast wird nun ein eine 0, wenn man links geht und eine 1 wenn man rechts geht, zugewiessen
Die Pfade zu allen Blätter aufschreiben. Das ist der Huffmancode

Lauflängenkodierung

Man speichert, wie oft ein Symbol vorkommt. Anstatt "AAAAAABBC" könnte man einfach "6A2B1C"

Um auch Symbole, welche nur einmal vorkommen, effizent zu speichern, wird ein Token benutzt, welcher symbolisiert, dass nun eine Lauflängenkodierung kommt.

Um das obere Beispiel nochmals aufzugreiffen: "Z6AZ2BC". Hier wurde Z als Marker (oder Token) gewählt, und nur wenn ein Z gelesen wird, wird das folgende als Länge interpretiert.

Wie viel Zeichen als Marker reserviert werden soll, ist abhängig von der Quelle in ihre statistischen Eigenschaften.

LZ77

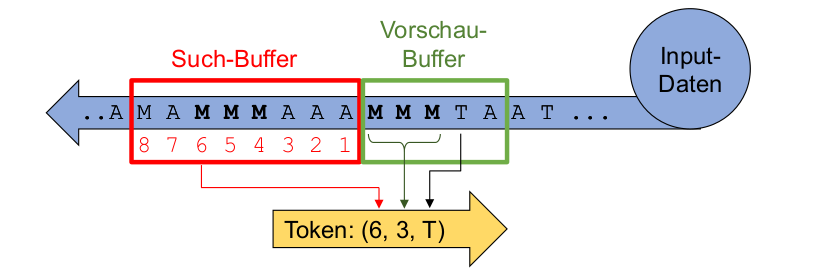
Ein Token ist definiert als (Offset, Länge, Zeichen). Es hat eine fixe Länge.

Es gibt ebenfalls ein Such- und ein Vorschau-Buffer. Es werden im Such-Buffer nach denselben Muster gesucht.

Falls ein Match gefunden wurde, wird ein Token geschrieben. In diesem ist der Offset des Such-Buffer, die Länge ist die Länge des Musters, und das Zeichen das nächste Zeichen nach dem gemachten Muster.

Falls kein Match gefunden wurde, wird folgender Token geschrieben (0, 0, Zeichen). Dies ist nötig, da zu Beginn des Algorithmus noch nichts im Such-Buffer ist.

Um dies zu dekodieren, wird dies Rückwärts durch gearbeitet

LZW

LZW bassiert auf LZ77 mit einigen Änderungen. Anstatt eines "Sliding Window" benützt man ein Wörterbuch. Ein Token besteht nur aus einem Index, welchen auf das Wörterbuch referenziert. Der Dekoder baut gleichzeitig mit den empfangenen Tokens das Wörterbuch auf.

Um ein Text zu enkodieren, werden folgende Schritte durchgeführt

Suche das aktuelle Zeichen im Wörterbuch
So lange verlängern, wie möglich und dieses als Token versenden
Ein neuen Eintrag Token + der nächste Zeichen ins Wörterbuch hinzufügen

Um nun einen Tokenstream wieder zu dekodieren, muss man folgendes tun:

Empfangener Token ausgeben
Empfangener Token ins Wörterbuch als neuer Eintrag hinzufügen (mit einem Blank am Ende)
Nächster empfangener Token ausgeben und die Blank vom letzten Schritt ausfüllen mit dem ersten ausgegeben Buchstaben des empfangen Tokens
Gehe zu Schritt 2