Register Allocation
Terms and definitions
- spilled: Writing a register into memory to free the register
- Liveness: A value is live between its definition and the uses of that value
- Live Range: The live range of a value is from its definition to its last use
MAXLIVEis the maximal number of values live at a point. If the number of live values is larger thanMAXLIVEthen the some values have to be spilled- Two values interfere with each other, if they are live simultaneously
Interference Graph
In an interference graph \(G_I\),
- Nodes represent values
- Edges represent two values interfering with each other
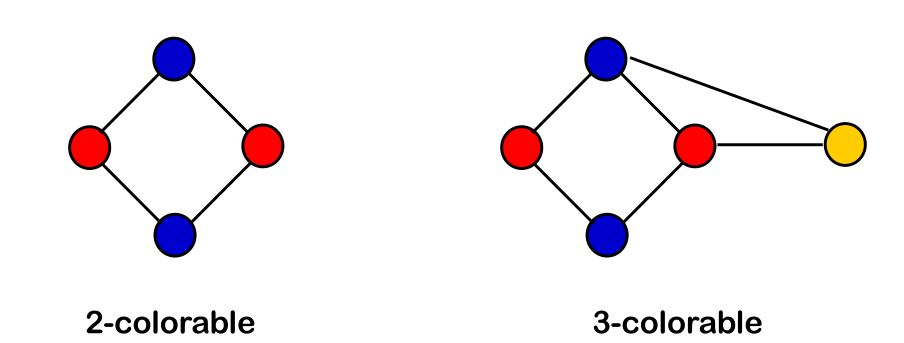
A interference graph \(G_I\) is said to be \(k\)-colourable iff (if an if only) the nodes can be labeld with integers \(1...k\), so that no edge in G connects two nodes with the same label. Each colour can be mapped to a register.
If an interference graph is not easily \(k\)-colourable, change the graph by breaking one live range into some ranges through spilling and splitting.
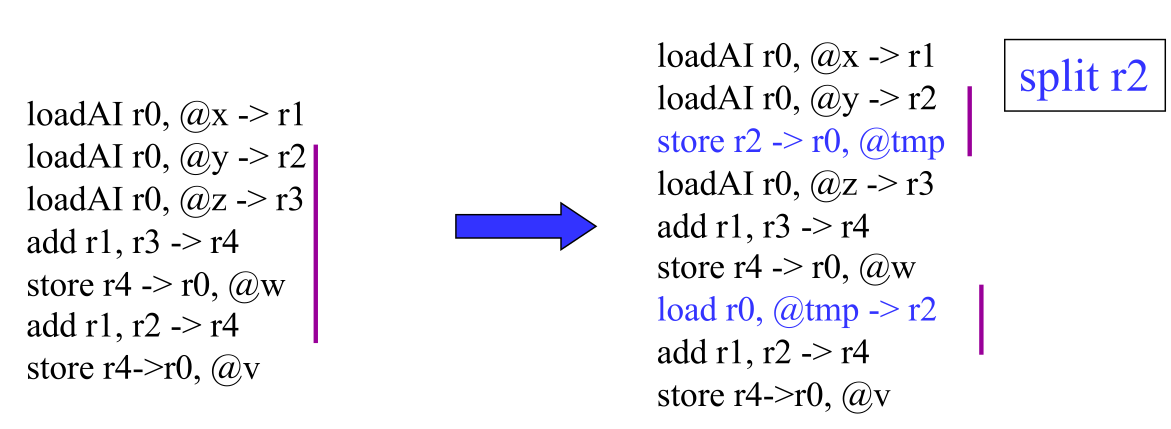
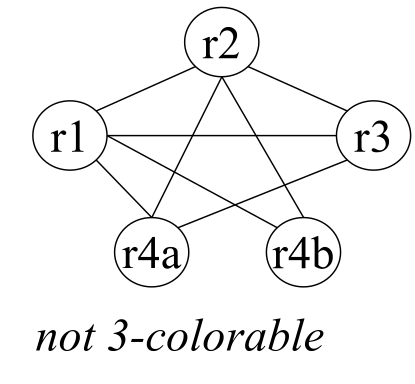
Splitting and Spilling
Splitting is when a live value is broken up into pieces larger than a single reference.
On the other hand, spilling is when a store instruction is inserted after every definition of the live value and a load instruction before each use. This can incur a higher runtime cost, but it breaks up the live value into more pieces. We hope that the spill stays in the cache, meaning that, paradoxically, a spilled value should be accessed frequently enough to keep it in the cache.
To decide if splitting or spilling is used, the compiler tries to estimate the cost of each:
- Spilling can be calculated with: \((addressComputationCost + memoryOperationCost)\cdot estimatedExecutionFrequency\)
Chaitin's Algorithm
- While existing vertices with \(< k\) neighbours in \(G_I\)
- Pick any vertex \(n\) whose degree is less than \(k\) and put it on the stack
- Remove that vertex and all edges incident to it from \(G_I\) (This will lower the degree of \(n\)'s neighbours')
- If \(G_I\) is still non-empty (all vertices have \(k\) or more neighbours), then:
- Pick a vertex \(n\) (using some heuristic) and spill the live range associated with \(n\)
- Remove vertex \(n\) from \(G_I\), along with all edges incident to it and put it on the stack
- If this causes some vertex in \(G_I\) to have fewer than \(k\) neighbours, then go to step 1; otherwise repeat step 2
- Successively pop vertices of the stack and colour them in the lowest colour not used by some neighbour (since the colours are ordered, the lowest colour is the "smallest" free color)
- Spill or split uncoloured nodes and build the new \(G_I\) and start over
TODO: Insert both example