STS Summary

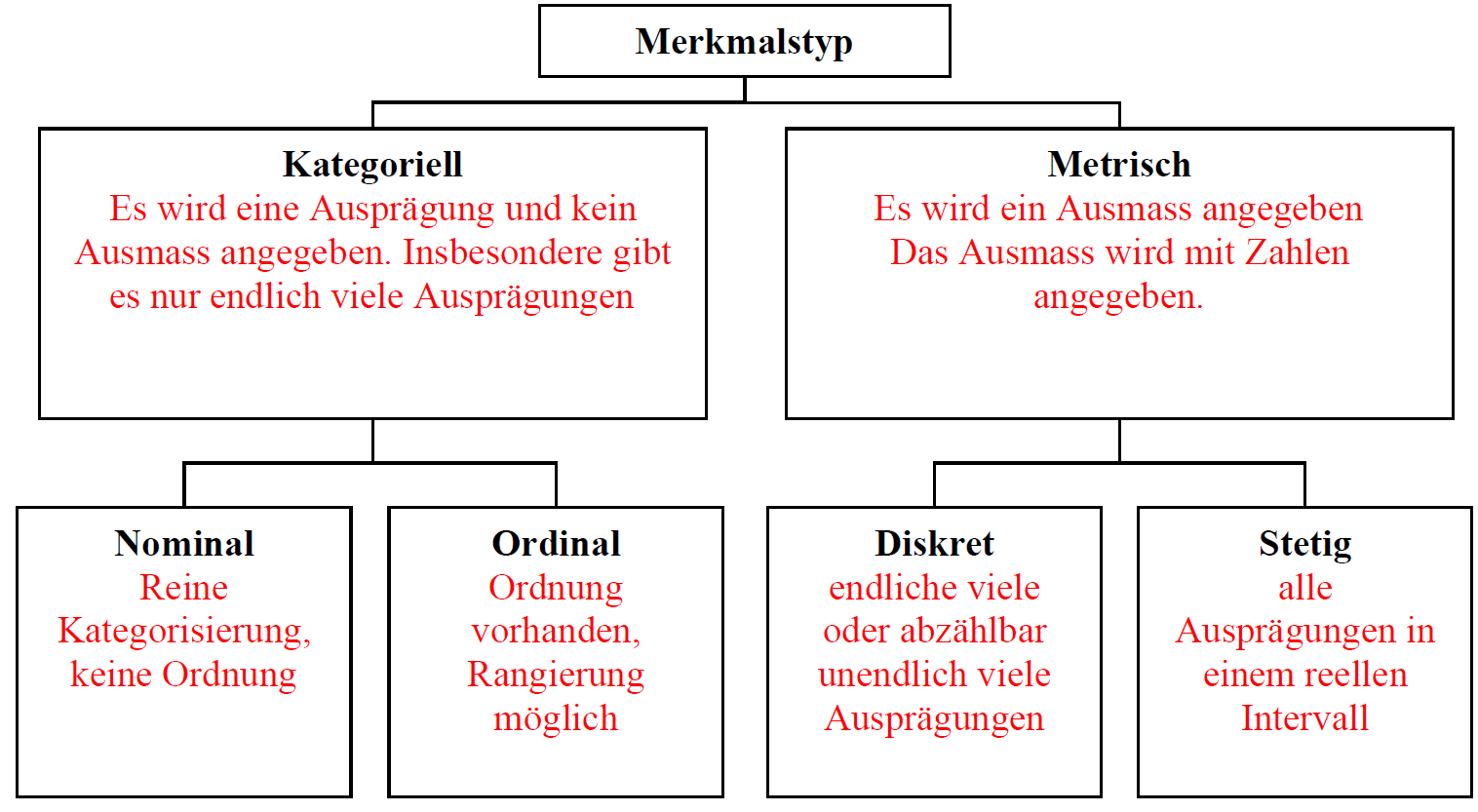
Deskriptive Statistik

Funktion	Nicht Klassiert	Klassiert
absolute Häufigkeit $h(x)$
relative Häufikeit (PMF) $f(x)$ / $g(x)$	$f(x)=\frac{h(x)}n$	$g(x)=f_i$
Dichtefunktion $f(x)$ ($b_i=$ Klassengrösse ) (PDF)	-	$f(x)=\frac{g(x)}{b_i}$
kummulative absolute Häufigkeit $H(x)$	$H(x)=\sum_{a_i \lt x}h_i$	-
kummulative relative Häufigkeit (CDF) $F(x)$	$F(x)=\sum_{a_i}f_i=\frac{H(x)}{n}$	$F(x)=\int^x_{-\infty}f(y)\mathrm d y$, $F(x)=F(a_i)+\frac{x-a_i}{a_{i+1}-a_i}\cdot (F(a_{i+1})-F(a_i))$
Modus $x_{mod}$	Höchste absolute Häufigkeit	gleich
Klassenmitte $M_i$	-	$M_i=\frac{a_{i+1}-a_i}{2}$
Stichprobenmittelwert $\overline x$	$\overline x=\frac 1 n\sum^n_{i=1}x_i$	$\overline x=\sum^n_{i=1}M_i\cdot f_i$
Varianz	$s^2 = \frac 1 n \sum^n_{i=1}(x_i - \overline x)^2 \\ = \frac 1 n \left (\sum^n_{i=1}x_i^2 \right)- \overline x ^2$	$s^2=\sum^n_{i=1}(M_i-\overline x)^2\cdot f_i$
Korrigierte Varianz	$s_{korr}^2=\frac 1 {n-1}\sum^n_{i=1}(x_i - \overline x)^2 \\ = \frac n {n - 1}s^2$	$s_{korr}^2= \frac n {n - 1}s^2$
(korrigierte) Standardabweichung $s$	$s_{korr}=\sqrt{s_{korr}^2}$	gleich
Kovarianz	$s_{xy}=\frac 1 n \sum^n_{i=1}(x_i-\overline x)\cdot (y_i- \overline y)\\= \left(\frac 1 n \sum^n_{i=1}x_iy_i\right)-\overline x \cdot \overline y$	-

Taschenrechner Befehle

Funktion	TR-Befehl
`stat-menu`	`shift` + `1` (`STAT`)
Varianz für `x`	`stat-menu` - `5: s-var` - `3: xσn`
Varianz für `y`	`stat-menu` - `5: s-var` - `6: yσn`
Korrigierte Varianz für `x`	`stat-menu` - `5: s-var` - `4: xσn-1`
Korrigierte Varianz für `y`	`stat-menu` - `5: s-var` - `7: xσn-1`
Durchschnitt für `x`	`stat-menu` - `5: s-var` - `2: x`
Durchschnitt für `y`	`stat-menu` - `5: s-var` - `5: y`
Pearson-Korrelationskoeffizient $r_{xy}$	`stat-menu` - `7: Reg` - `3: r`
Regressions-Gerade $B * x + A$	`stat-menu` - `7: Reg` - `1: A`, `stat-menu` - `7: Reg` - `2`

Quantile / Boxplot

\[ \text{Nicht klassiert:}\\ R_q=\begin{cases} \frac{x_{[n \cdot q]}+x_{[n\cdot q + 1]}}{2} & n \cdot q \text{ ganze Zahl}\\ x_{[\lceil n\cdot q\rceil]} & n\cdot q \text{ keine ganze Zahl} \end{cases}\\\\ \text{klassiert:}\\ R_q=\frac{b - a}{F(b) - F(a)}\cdot (q - F(a)) + a \]

Note:
Für $a$ als die untere und $b$ als die obere Grenze der Klasse, welche das Quantil beinhaltet.

Die Klasse, welche das Quantil beinhaltet, ist die erste Klasse, dessen CDF $q$ überschreitet.

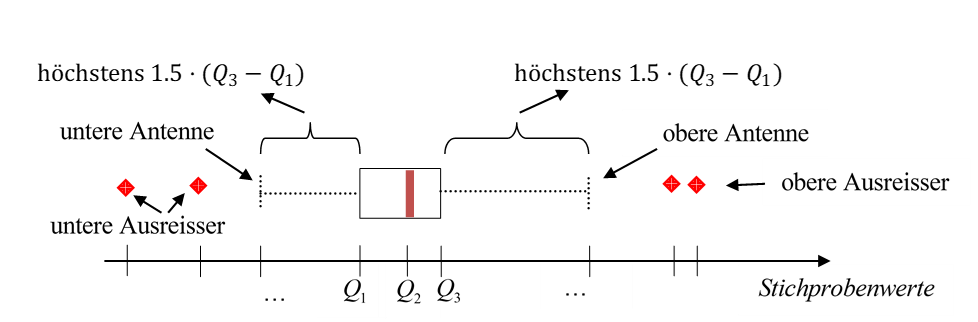
$IQR=Q_3-Q_1$

Pearson-Korrelationskoeffizient

\[ r_{xy}=\frac{S_{xy}}{S_x\cdot S_y}=\frac{\overline{xy}-(\overline x \cdot \overline y)}{\sqrt{\overline{x^2}-\overline x^2}\cdot \sqrt{\overline {y^2}-\overline y ^2}} \]


$r_{xy}\approx 1$	Positiver Linearer Zusammenhang
$r_{xy}\approx -1$	Negatiber Linearer Zusammenhang
$r_{xy}\approx 0$	Punkte sind gleichmässig um den Schwerpunkt $(\overline x, \overline y)$ verteilt

Der Pearon-Korrelationskoeffizient ist nicht robust und kann durch Ausreisser stark beeinflusst werden.

Spearman-Rangkorrelationskoeffizient

\[ \DeclareMathOperator{\rg}{rg} r_{Sp}=\frac{\sum^n_{i=1}(\rg(x_i) - \overline{\rg(x)})\cdot(\rg(y_i)-\overline{\rg(y)})} {\sqrt{\sum^n_{i=1}(\rg(x_i) - \overline{\rg(x)})^2} \cdot \sqrt{\sum^n_{i=1}(\rg(y_i) - \overline{\rg(y)})^2}}\\ \rg(x_i)=1+Anzahl(j \vert x_j < x_i) + \frac 1 2 Anzahl(j | x_j = x_i, i \neq j) \]

Deutsch: $1$ $+$ die Anzahl von Elementen $x_j$, welche kleiner als $x_i$ sind $+$ die halbe Anzahl von Elementen, welche gleich sind, wie $x_i$.

Wenn es doppelte $x$- oder $y$-Elemente gibt, dann wird von verbundenen Rängen gesprochen, wobei der Durchschnitt der Ränge berechnet wird.

Der Spearman-Rangkorrelationskoeffizient misst, ob die Daten eine Korrelation mit einer strengen monotonen Funktion haben (eine Funktion, welche immer steigt oder fällt)

TODO: Multivariate Daten darstellen

Kombinatorik

Binomialkoeffizient: $\begin{pmatrix}n \\k \end{pmatrix}=\frac{n!}{(n-k)!\cdot k!}$ Wieviele Möglichkeiten gibt es $k$ Objekte von $n$ Objekten auszuwählen?

$n$ sind die Anzahl Optionen, $k$ wieviele gewählt werden.

Kombination mit Wiederholung: $k$ Objekte aus $n$ möglchen Sorten/Töpfen

Beispiele:

Anzahl Möglichkeiten für eine beliebig grosse Gruppe mit 20 potenziellen Personen: $2^{20}-1$ Jede Person ist entweder in der Gruppe oder nicht und $-1$ wegen der Leeren Gruppe

Wahrscheinlichkeit

\[ \text{Zähldichte: } \rho: \Omega \to [0, 1]\\ \text{Wahrscheinlichkeitsmass: } P: 2^\Omega \to [0, 1], P(M)=\sum_{\omega \in M} \rho(\omega) \]

Der Wahrscheinlichkeitsraum $(\Omega, P)$ wird Laplace-Raum genannt, wenn alle Ereignisse gleich wahrscheinlich sind.

$P(X=x)=f(x)$
$P(X \le x)=F(x)$
$P(a \le X \le b)=P(X\le b)-P(X\le a)$
$P(X > x)=1-P(X\le x)$

Kenngrössen

Lagemass: Was ist das Zentrum Streumass: Die Verteilung des Merkmals

Erwartungswert $E(X)=\sum_{x\in\R}P(X=x)\cdot x$
$E(X+Y)=E(X)+E(Y)$ und $E(\alpha X) = \alpha E(X)$
Varianz $V(X)=E(X^2)-(E(X))^2 = E((X-E(X)^2)=\\(\sum_{x\in\R}P(X=x)\cdot x^2)-E(X)^2=\sum_{x\in\R}P(X=x)\cdot(x-E(X))^2$

Bedingte Wahrscheinlichkeit

Eintreten von $B$, wenn $A$ eingetroffen ist (Satz von Bayes): $P(B\vert A) = \frac{P(A\cap B)}{P(A)}=\frac{P(A\vert B)\cdot P(B)}{P(A)}$
Multiplikationssatz: $P(A\cap B)=P(A\vert B)\cdot P(B)=P(B\vert A)\cdot P(A)$
Satz von der Totalen Wahrscheinlichkeit: $P(A)=P(A\vert B)\cdot P(B) + P(A|\overline B)\cdot P(\overline B)$

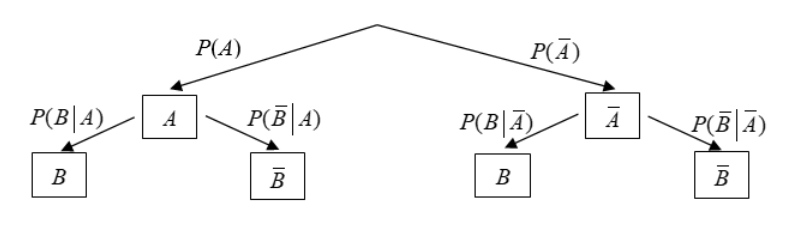
Vierfeldertafel

Die Ereignisse in einer Vierfeldertafel müssen Disjunkt sein.

Stochastische Unabhängigkeit

Zwei Ereignisse $A$ und $B$ sind stochastisch unabhängig, wenn gilt $P(A\cap B)=P(A)\cdot P(B)$.

Wenn $A$ und $B$ stochastisch unabhänig sind:

sind auch $\overline A$ und $\overline B$, wie $\overline A$ mit $B$ und $A$ mit $\overline B$ unabhängig
gilt $P(A\vert B)=P(A)$ und $P(B\vert A)=P(B)$
gilt $E(X\cdot Y)=E(X)\cdot E(Y)$ und $V(X+Y)=V(X) + V(Y)$

Um zu überprüfen ob $n$ Ereignisse unabhänig sind, braucht es $2^n - n -1$ Gleichungen, da sie disjunkt unabhängig sein müssen.

Spezielle Verteilungen

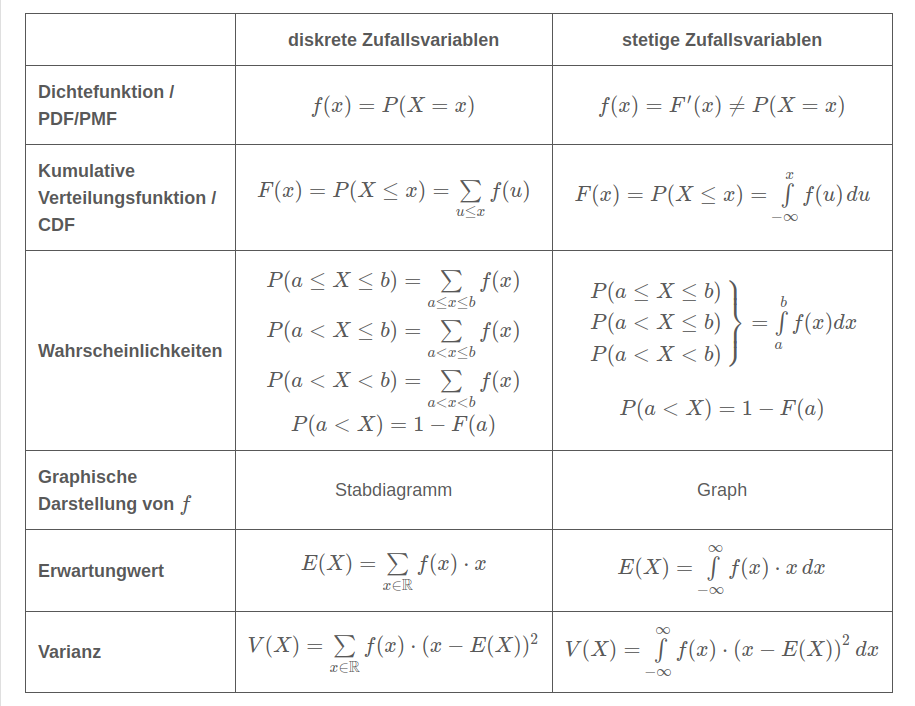
Hypergeometrische Verteilung ($X \sim H(N, M, n)$)

Es gibt eine Urne mit $N$ Objekte, von welchen $M$ einer bestimmten Sorte angehöhren ($N- M$ gehöhren zu anderen Sorten). Zufällig wird eine Stichprobe von $n$ Objekten aus der Urne genommen. Wichtig ist, dass sie nicht Zurückgelegt werden.

Die Zufallsvariable $X$ beschriebt die Anzahl von Objekten von der Sorte $M$. Es gilt $X \sim H(N, M, n)$

\[ P(X=x)=\frac{\begin{pmatrix}M\\x\end{pmatrix}\cdot \begin{pmatrix}N - M\\n - x\end{pmatrix}} {\begin{pmatrix}N\\n\end{pmatrix}}\\ \]

\[ \begin{align} \mu=E(X)&=n\cdot \frac M N\\ \sigma^2=V(X)&=n\cdot \frac M N \cdot (1 - \frac M N) \cdot \frac{N - n}{N - 1}\\ \sigma = S(X)&=\sqrt{n\cdot \frac M N \cdot (1 - \frac M N) \cdot \frac{N - n}{N - 1}} \end{align} \]

Bernoulliverteilung

Ein Bernoulli-Expermient, ist ein Zufallsexperiment, inwelchem es nur zwei Möglichkeiten gibt.

\[ \begin{align} P(X=1)&=p\\ P(X=0)&=1-p=q\\ \end{align} \]

\[ \begin{align} E(X)&= P(X=1)=p\\ E(X^2)&= P(X=1) = p\\ V(X)&=E(X^2)-(E(X))^2=p - p^2 \end{align} \]

Binomailverteilung ($X\sim B(n, p)$)

Wenn ein Bernoulliexperiment $n$-mal wiederholt wird und die Wahrscheinlichkeit für $P(X=1)=p$ ist und $q=1-p$. Die Wiederholungen müssen stochastisch unabhängig sein.

Es gilt $X\sim B(n, p)$

\[ P(X=x)=\begin{pmatrix}n\\x\end{pmatrix}\cdot p^x\cdot q^{n-x} \]

\[ \begin{align} \mu=E(X)&=np\\ \sigma^2=V(X)&=npq\\ \sigma = S(X)&=\sqrt{npq} \end{align} \]

Wenn gilt $n \lesssim \frac N {20}$, dann kann die eine hypergeometrische Verteilung mit einer Binomialverteilung angenähert werden: $H(N, M, n)\approx B(n, \frac M N)$

Poissonverteilung ($X\sim P(\lambda)$)

Die Poissonverteilung kann als stochastisches Modell benutzt werden, wenn es um die Wahrscheinlichkeit für das Eintreten einer bestimmten Anzahl gleichartiger Ereignisse geht, welche in einem gegebenen Bereich $\lambda$ (unabhängig voneinander) beliebig oft auftreten können.

\[ P(X=x)=\frac{\lambda^x}{x!}\cdot e^{-\lambda} \]

\[ \begin{align} \mu=E(X)&=\lambda\\ \sigma^2=V(X)&=\lambda\\ \sigma = S(X)&=\sqrt{\lambda} \end{align} \]

Für eine Binomialverteilung, wenn $n$ gegen unendlich geht und $\lambda=n \cdot p$ konstant ist, dann kann eine Binomialverteilung mit einer Poissonverteilung approximiert werden: $B(n, p)\xrightarrow{n\to \infty \text{ und } \lambda=np \text{ konstant}} Poi(\lambda)$

Ebenfalls wenn $n \gtrsim 50$ und $p\lesssim 0.1$, dann kann eine Binomialverteilung mit einer Poissonverteilung approximiert werden: $B(n, p)\approx Poi(n\cdot p)$

Gauss'sche Verteilung ($X\sim N(\mu, \sigma)$ / $X\sim N(0, 1)$)

\[ \begin{align} \text{PDF: }\varphi_{\mu,\sigma}(x)&=\frac{1}{\sqrt{2\pi}\cdot\sigma}\cdot e^{-\frac1 2\cdot (\frac{x-\mu}{\sigma})^2}\\ \text{CDF: }\phi_{\mu, \sigma}(x)&=\int^x_{-\infty}\varphi_{\mu, \sigma}(t)\mathrm dt0 =\frac 1 {\sqrt{2\pi}\cdot \sigma}\cdot \int^x_{-\infty}e^{-\frac 1 2(\frac{t-\mu}{\sigma})^2}\mathrm dt \end{align} \]

Wenn $\mu=0$ und $\sigma = 1$ ist, dann wird von einer Standardnormalverteilung gesprochen und wird einfach als $\varphi(x)$ bezeichnet:

$$ \varphi(x)=\frac 1 {\sqrt{2\pi}}\cdot e^{-\frac 1 2 x^2} $$ Um eine "normale" Gauss'sche Verteilung zu standardisieren, wird anstatt der Zufallsvariable $X$ folgende Definition $U=\frac{X-\mu} \sigma$ verwendet.

Der Erwartungswert $\mu$ und Standardabweichung $\sigma$ sind Parameter.

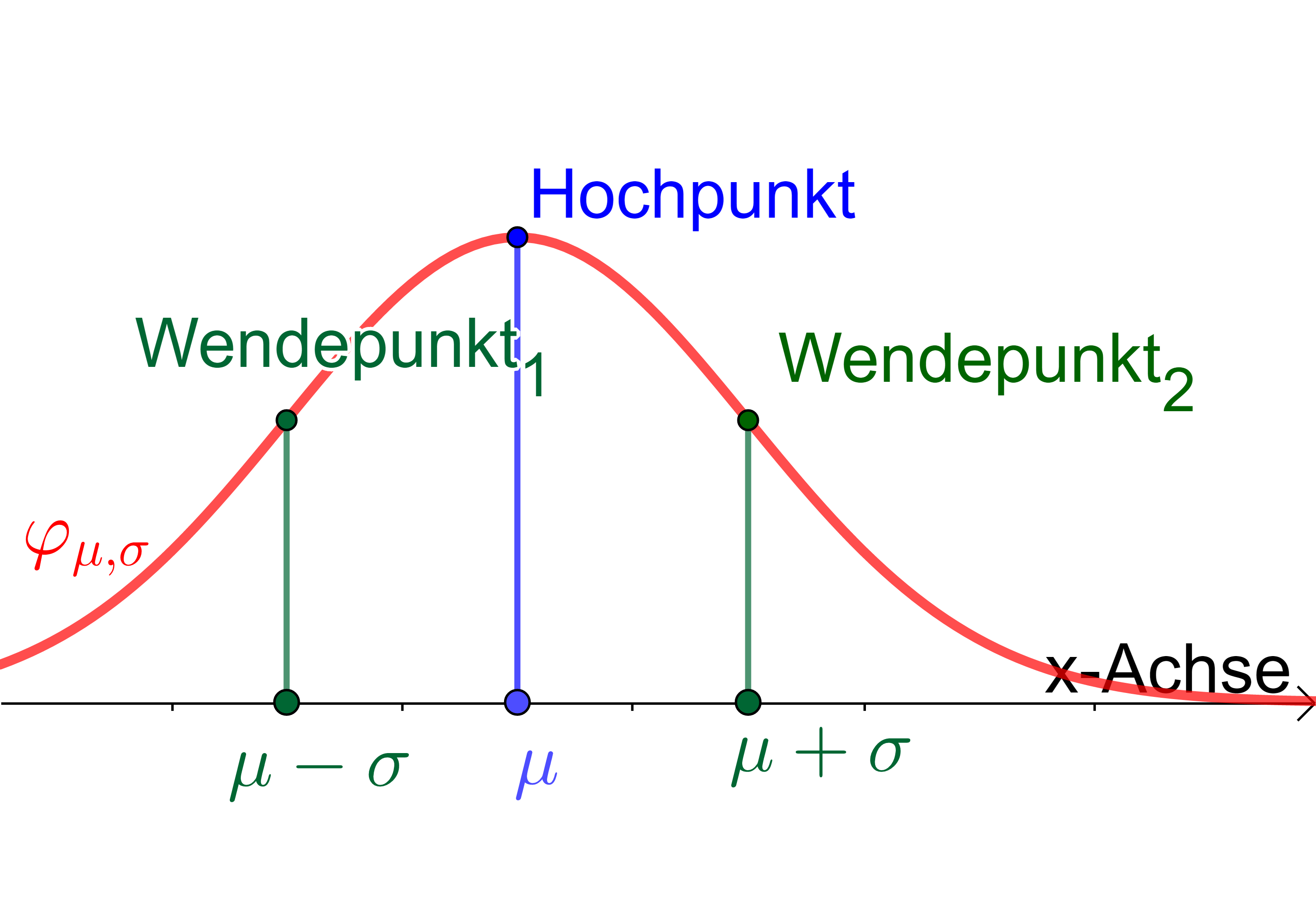
Eine Normalverteilung hat folgende Eigenschaften:

Ist Symetrisch bei der Geraden $x=\mu$
Hat Wendepunkte bei $\mu-\sigma$ und $\mu + \sigma$
Ist normiert (totale Fläche unter der Kurve = 1)
Je grösser $\sigma$, desto breiter und niedriger wird die Glockenkurve
Eine Änderung von $\mu$ verschiebt die Kurve in der x-Richtung
$P(a \le X \le b) = P(a < X < b) = \phi_{\mu, \sigma}(b)-\phi_{\mu, \sigma}(a)$
$P(\vert X - \mu \vert \le \varepsilon)=P(\mu - \varepsilon \le X \le \mu + \varepsilon)=2\cdot \phi_{\mu, \sigma}(\mu + \varepsilon) - 1= 1 - 2\cdot \phi_{\mu,\sigma}(\mu - \varepsilon)$

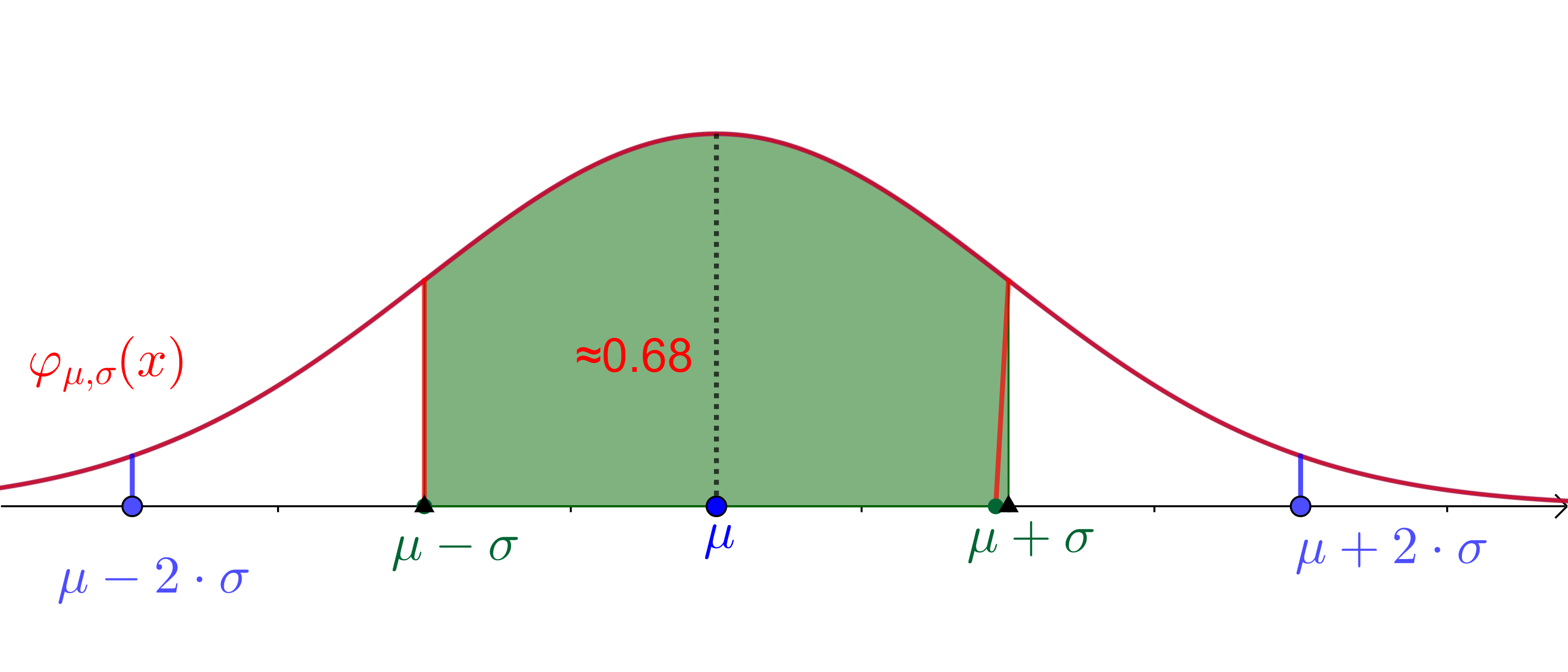
Für die Verteilung $N(\mu, \sigma)$, liegen

ca. 68% der Werte zwischen $\mu-\sigma$ und $\mu + \sigma$
ca. 95% der Werte zwischen $\mu-2\sigma$ und $\mu + 2\sigma$
ca 99.7% der Wete zwischen $\mu-3\sigma$ und $\mu + 3\sigma$

Approximationen

Was	Bedingung	Approximation
$X\sim B(n, p)$	$npq>9$	$P(a\le X \le b)=\sum^b_{x=a}P(X=x)\approx \phi_{\mu, \sigma}(b+\frac 1 2)-\phi_{\mu,\sigma}(a-\frac 1 2)$
$X\sim P(\lambda))$	$x > 9$	$P(a \le X \le b)=\sum^b_{x=a}P(X=x)\approx \phi_{\mu, \sigma}(b+\frac 1 2)-\phi_{\mu,\sigma}(a-\frac 1 2)$

Zentraler Grenzwertsatz

Wenn mehrere stochastisch unabhängige Zufallsvariabeln denselben Erwartungswert $\mu$ und dieselbe Varianz $\sigma ^2$ haben, dann gilt für die Summe $S_n=\sum^n_{i=1}X_i$ der Zufallsvariabeln folgendes:

$E(S_n)=n\mu$
$V(S_n)=n\sigma^2$

Zusätzlich gilt, dass die Vertielungsfunktion $F_n(u)$ der standartisierten Zufallsvariable

$$ U_n=\frac{(X_1 + X_2 +...+X_n)-n\mu}{\sqrt n \cdot \sigma}=\frac{\overline X - \mu}{\frac \sigma {\sqrt{n}}}\ \overline X = \frac {S_n} n $$ für $n\to\infty$ gegen die Verteilungsfunktion $\phi(u)$ der Standardnormalverteilung konvergiert.

Es kann ebenfalls gesagt werden, dass das arithmetische Mittel $\overline X_n$ von $n$ identisch verteilten, unabhänigen Zufallsvariablen näherungsweise $N(\mu, \frac \sigma {\sqrt n})$ verteilt ist.

Regression

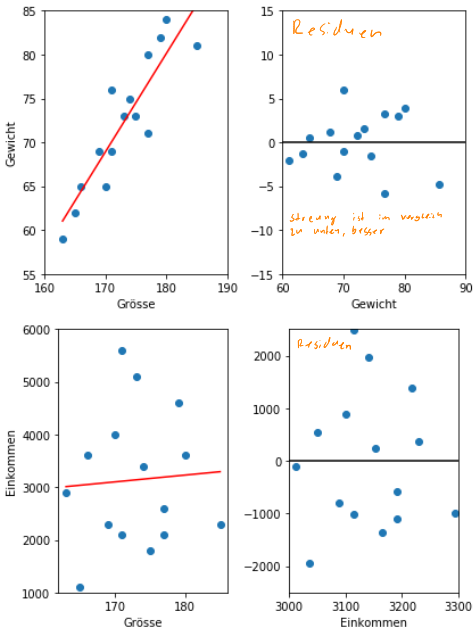
Das Ziel einer Regressions-Gerade $g=m\cdot x + d$ ist es, den Residuen (oder Fehler) $\sum^n_{i=1} (y_i-g(x_i))^2$ zu minimieren.

\[ m=\frac{S_{xy}}{S_x^2}{}\\ d=\overline y - m\overline x\\ S_\epsilon^2=S_y^2-\frac{S_{xy}^2}{S_x^2} \]

$S_{xy}$ ist die Kovarianz, $S_x^2$ ist die (nicht korrigierte) Varianz, $S_\epsilon^2$ ist die Residualvarianz

Bestimmtheitsmass

\[ \begin{align} S_y^2&=S_\epsilon^2 + S_{\hat y}^2\\ R^2&=\frac{S_{\hat y}^2}{S_y^2}\\ R^2&=\frac{S_{xy}^2}{S_x^2\cdot S_y^2}=r_{xy}^2 \\ \sqrt R=\sqrt{r_{xy}}&=\text{Pearson-Korrelationskoeffizient} \end{align} \]

Das Bestimmheitsmass ist zwischen 0 und 1 und gibt an, wieviel Prozent der Varianz durch $R^2$ erklärt wird. 0 heisst dass die Gerade nicht passt. 1 heisst, dass die Gerade perfekt passt. Wenn $R^2=0.75$ ist, bedeutet dies, dass 75% der gesamten Varianz durch die Regressionsgerade erklärt wird und 25% ist zufallsbedingt.

Linearisieren

Eine nicht lineare Funktion kann linearisiert werden. Danach ist sie linear und kann durch eine Regressions-Gerade angenähert werden.

Matrizen

Gegeben sind $n$ Gleichungen und es sind $k$ Regressionsparameter $x_1$, $x_2$, ..., $x_k$ gesucht.

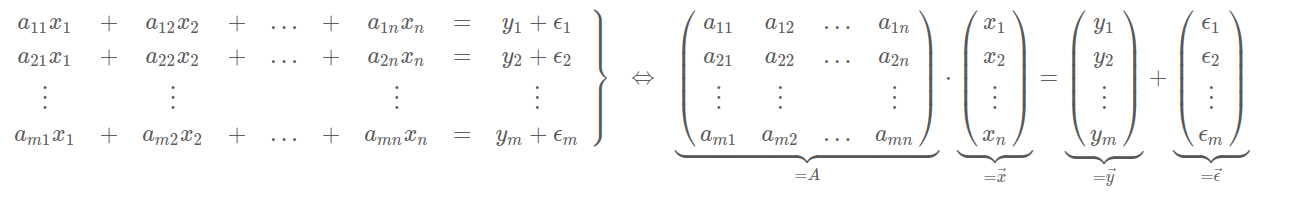
Die Lösung für $\vec x$ ist: $\vec x=(A^TA)^{-1}X^T\vec y$

Schliessende Statistik

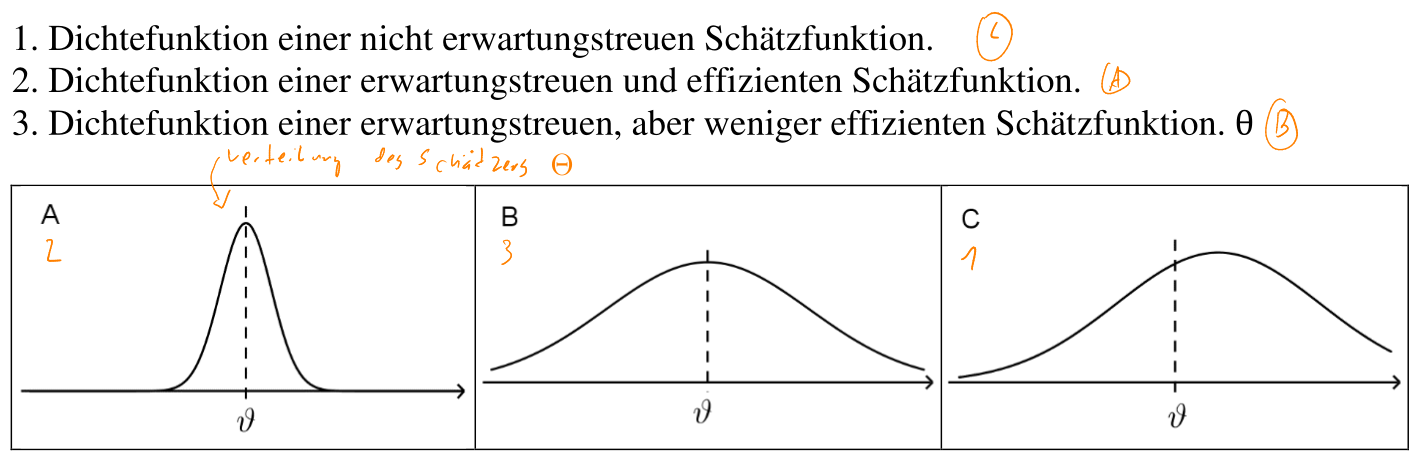
$\Theta=g(X_1, X_2, ..., X_n)$ ist eine Funktion, welche von $n$ Stichprobenvariabeln die Grundgesammtheit schätzen kann. Ein Schätzwert wird als $\hat \theta$ bezeichnet. $\theta$ (ohne Dach) ist der eigentliche, unbekannte Wert/Parameter.

$\overline X$ und $S^2$ sind erwartungstreu ($E(\Theta)=\theta$) und konsistent. $S$ ist konsitent ($E(\Theta)\to \theta$ und $V(\Theta)\to 0$ für $n\to \infty$) aber nicht erwartungstreu.

Eine Schätzfunktion $\Theta_1$ ist effizienter als $\Theta_2$ wenn gilt $V(\Theta_1) < V(\Theta_2)$

Vertrauensintervalle

Es werden zwei Stichprobenfunktionen $\Theta_u$ und $\Theta_o$ bestimmt, welche den wahren Wert $\theta$ mit einer vorgegebenen Wahrscheinlichkeit von $\gamma$ einschliesst.

\[ P(\Theta_u \le \theta \le \Theta_o)=\gamma \]

Wenn konkrete Werte in $\Theta_u$ und $\Theta_o$ eingesetzt werden, dann wird das Intervall $[c_u; c_o]$ gebildet. $\gamma$ heisst das Vertrauensniveau (oder statistische Sicherheit) und $\alpha = 1 - \gamma$ ist die Irrtumwahrscheinlichkeit.

In der folgenden Tabelle sind die mathematischen Zeichen von oben erklärt:

Zeichen	Bedeutung
$\mu$	Durchschnitt / Mittel
$\sigma$, $S$	Standardabweichung
$\sigma^2$, $S^2$	Varianz
$p$, $q$	Wahrscheinlichkeits-Wert

Funktion	Nicht Klassiert	Klassiert
absolute Häufigkeit \(h(x)\)
relative Häufikeit (PMF) \(f(x)\) / \(g(x)\)	\(f(x)=\frac{h(x)}n\)	\(g(x)=f_i\)
Dichtefunktion \(f(x)\) (\(b_i=\) Klassengrösse ) (PDF)	-	\(f(x)=\frac{g(x)}{b_i}\)
kummulative absolute Häufigkeit \(H(x)\)	\(H(x)=\sum_{a_i \lt x}h_i\)	-
kummulative relative Häufigkeit (CDF) \(F(x)\)	\(F(x)=\sum_{a_i}f_i=\frac{H(x)}{n}\)	\(F(x)=\int^x_{-\infty}f(y)\mathrm d y\), \(F(x)=F(a_i)+\frac{x-a_i}{a_{i+1}-a_i}\cdot (F(a_{i+1})-F(a_i))\)
Modus \(x_{mod}\)	Höchste absolute Häufigkeit	gleich
Klassenmitte \(M_i\)	-	\(M_i=\frac{a_{i+1}-a_i}{2}\)
Stichprobenmittelwert \(\overline x\)	\(\overline x=\frac 1 n\sum^n_{i=1}x_i\)	\(\overline x=\sum^n_{i=1}M_i\cdot f_i\)
Varianz	\(s^2 = \frac 1 n \sum^n_{i=1}(x_i - \overline x)^2 \\ = \frac 1 n \left (\sum^n_{i=1}x_i^2 \right)- \overline x ^2\)	\(s^2=\sum^n_{i=1}(M_i-\overline x)^2\cdot f_i\)
Korrigierte Varianz	\(s_{korr}^2=\frac 1 {n-1}\sum^n_{i=1}(x_i - \overline x)^2 \\ = \frac n {n - 1}s^2\)	\(s_{korr}^2= \frac n {n - 1}s^2\)
(korrigierte) Standardabweichung \(s\)	\(s_{korr}=\sqrt{s_{korr}^2}\)	gleich
Kovarianz	\(s_{xy}=\frac 1 n \sum^n_{i=1}(x_i-\overline x)\cdot (y_i- \overline y)\\= \left(\frac 1 n \sum^n_{i=1}x_iy_i\right)-\overline x \cdot \overline y\)	-


\(r_{xy}\approx 1\)	Positiver Linearer Zusammenhang
\(r_{xy}\approx -1\)	Negatiber Linearer Zusammenhang
\(r_{xy}\approx 0\)	Punkte sind gleichmässig um den Schwerpunkt \((\overline x, \overline y)\) verteilt

Was	Bedingung	Approximation
\(X\sim B(n, p)\)	\(npq>9\)	\(P(a\le X \le b)=\sum^b_{x=a}P(X=x)\approx \phi_{\mu, \sigma}(b+\frac 1 2)-\phi_{\mu,\sigma}(a-\frac 1 2)\)
\(X\sim P(\lambda))\)	\(x > 9\)	\(P(a \le X \le b)=\sum^b_{x=a}P(X=x)\approx \phi_{\mu, \sigma}(b+\frac 1 2)-\phi_{\mu,\sigma}(a-\frac 1 2)\)