Introduction
Kerckhoffs’ Principle
Design your system to be secure even if the attacker has complete knowledge of all its algorithms.
Properties of Ciphers
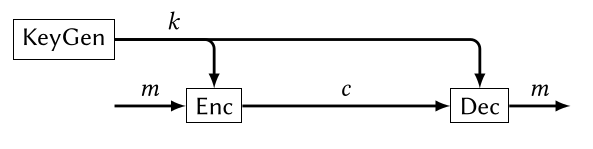
A private-key encryption scheme is defined by a message space \(\mathcal M\) (all legal messages) and three algorithms for generating keys (\(Gen\)), encrypting (\(Enc\)) and decrypting (\(Dec\)). valid
The set of all possible keys is the key space denoted by \(\mathcal K\).
A cipher should have the following properties:
- Correctness: \(Dec(k, Enc(k, m)) = m\)
One-Time Pad
One-time pad is essentially "just" xor-ing the message \(m\) with the key \(k\).
- Correctness: The following claim \(\forall k, m \in \{0, 1\}^\lambda (Dec(k, Enc(k, m)) = m)\) can be proven by applying properties of xor: $$ \begin{align} Dec(k, Enc(k, m)) & = Dec(k, k \oplus m)\ & = k \oplus k \oplus m \ & = (k \oplus k) \oplus m \ & = 0^\lambda \oplus m \ &= m \end{align} $$