Textsuche

Bruteforce

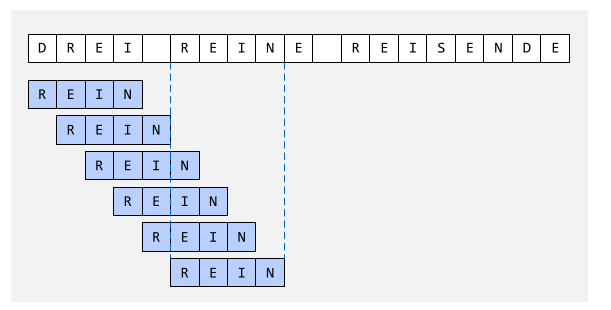
Der Aufwand des folgenden Algorithmus ist \(O(n\cdot m)\), wobei \(n\) die Anzahl Zeichen im String und \(m\) die Anzahl Zeichen im Pattern sind.

static int indexOf(String str, String pattern) {
    int k;
    for (int i = 0; 
         i < str.len() - pattern.len() + 1; 
         i++) 
    {

        // Sucht den ersten übereinstimmenden Buchstaben
        while (i < str.len() 
               && str.charAt(i) != pattern.charAt(0)) 
        {
            i++;
        }

        if (i + pattern.len() <= str.len()) {
            for (k = 0; k < pattern.len() && str.charAt(i+k) == pattern.charAt(k); k++) {}
            if (k == pattern.len()) {
                return i;
            }
        }
    }
    return -1;
}

Knuth-Morris-Pratt Algorithmus

Dieser Algorithmus hat den Aufwand \(O(n+m)\). Der Algorithmus ist sinvoll, wenn das Pattern viele Wiederholungen hat oder wenn das Rückspringen aufwändig ist (z.B. bei externen Speichermedien)

Der Knuth-Morris-Pratt Algorithmus wird in zwei Schritten ausgeführt:

Phase 1: Next-Tabelle bauen

Der Aufwand dieser Phase ist \(O(m)\), wobei \(m\) die Länge des Pattern ist

1. Subpattern (mögliche Präfixe)
2. 

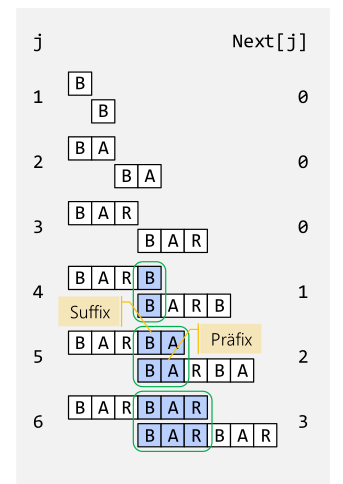
Nun folgt einen effizienteren Algorithmus:

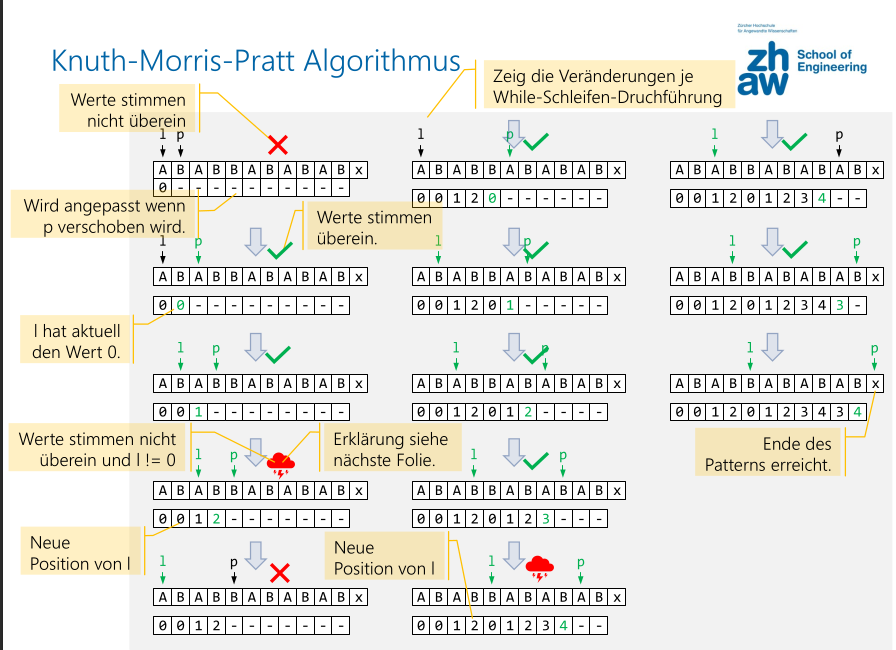
Es gibt drei Situationen:

1. str[l] == str[p]:
2. str[l] != str[p] && l == 0:
3. str[l] == str[p] && l > 0:

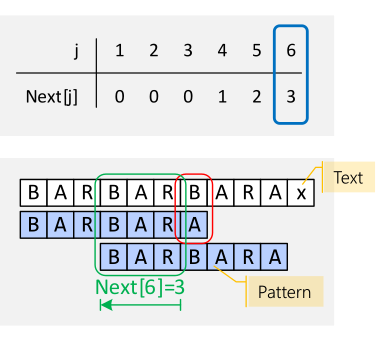
Phase 2: Suche

Diese Phase hat den Aufwand von \(O(n)\), wobei \(n\) die Länge des Text ist

Invertierter Index

Es wird einen Index geführt, welche Wörter wo vorkommen (z.B. banana kommt im dritten Text an vierter Stelle vor).

Es gibt mögliche Verbesserungen:

• Wörter sortieren und einen binären balancierten Baum benützten: \(O(\log(n))\)
• Hashtabelle: \(O(1)\)
• Stopwords entfernen (z.B. denn, die, ...)
• Wörter normalisieren: Wortstamm bilden (wohn: wohnen, bewohnen, Wohnzimmer, ...)

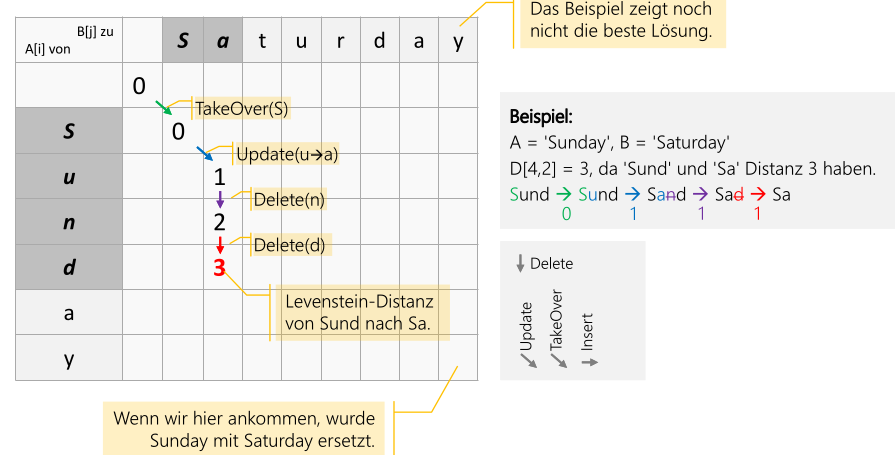
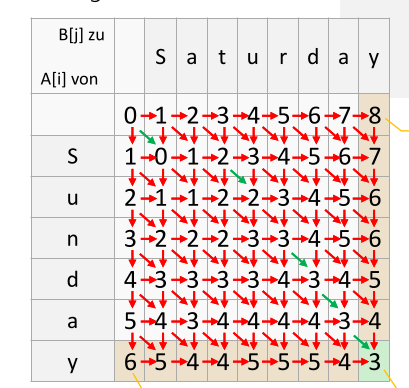
Levenshtein-Distanz

Die Levenshtein-Distanz ist die minimale Anzahl Operationen um von Wort-A Wort-B zu erreichen und kann somit als Mass verwendet werden, wie Ähnlich zwei Wörter sind.

Die folgenden Operationen sind erlaubt:

• doNothing(): Der Buchstabe wird übernommen
• insert(c): Ein Buchstabe an einer Position einfügen
• update(c -> d): Ein Buchstaben an einer Position ersetzten
• delete(c): Ein Buchstaben löschen

public static int computeLevenshteinDistance(String str1,String str2) {
    int[][] distance = 
        new int[str1.len() + 1][str2.len() + 1];

    // initialisierung
    for (int i = 0; i <= str1.len(); i++)
        distance[i][0] = i;
    for (int j = 1; j <= str2.len(); j++) 
        distance[0][j] = j;

    for (int i = 1; i <= str1.len(); i++) {
        for (int j = 1; j <= str2.len(); j++) {
            int minEd = (str1.charAt(i - 1) == str2.charAt(j - 1)) ? 0 : 1;
            distance[i][j] = minimum(distance[i - 1][j] + 1,
            distance[i][j - 1] + 1, distance[i - 1][j - 1]+ minEd);
        }
    }
    return distance[str1.len()][str2.len()];
}

Trigramm-Suche

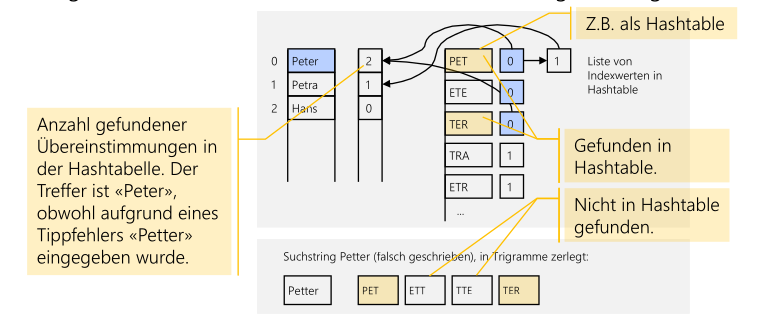
Phonetische Suche

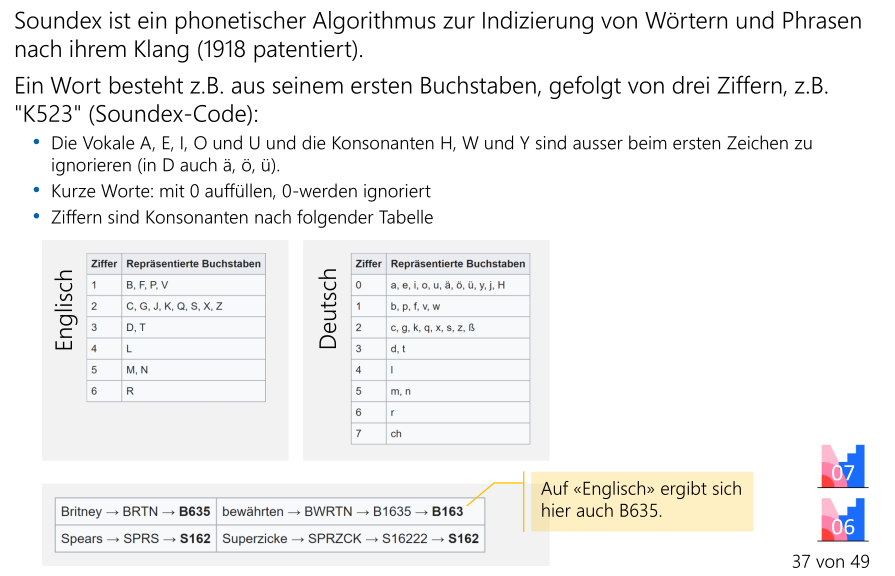
Regex

Mit Pattern pattern = Pattern.compile(String patternStr) kann ein Pattern vorbereitet werden.

// create Pattern object
Pattern pat = Pattern.compile("ZHAW");
// do the actual matching
Matcher matcher = pat.matcher("Willkommen an der ZHAW");

// find() finds the next match
while (matcher.find()) {
    String group = matcher.group(); // the found string
    int start = matcher.start(); // the start position
    int end = matcher.end(); // the end position
}

Platzhalter	Bedeutung	Beispiel
.	Ein beliebiges Zeichen
\d	Digit [0-9]
\D	Keine Digit
\w	ein Buchstabe, eine Ziffer oder einen Unterstrich
\W	Weder Buchstaben, Ziffer, noch Unterstrich
\s	Leerzeichen (Blank, etc)
\S	Kein Leerzeichen
[^s]	Alle Zeichen, ausser in s enthaltene Zeichen
s?	s kann 0 oder einmal auftreten
s*	s kann 0 oder mehrmals auftreten
s+	s muss 1 oder mehrmals auftreten
s{n}	s muss n-mal auftreten
s{m, n}	s muss mindestens m-mal und maximal n-mal auftreten