AN Summary 26.01.2022

AN Summary 26.01.2022

Begriff	Erklärung
gerade Funktion	Wenn der Graph achsensymmetrisch mit der y-Achse ist (wie bei $x^2$)
ungerade Funktion	Wenn der Graph punktsymmetrisch mit dem Nullpunkt ist (wie bei $x^3$)
Komposition	$(g\circ f)(x)=g(f(x))$
Injektive Funktion	Keine zwei $x$ führen zum selben $y$. Von einer injektiven Funktion gibt es eine Umkehrfunktion.
$\sum^5_{k=1}a_k$	Addiert $a_k$ bis (inklusiv) $5$: $a_1+a_2+a_3+a_4+a_5$
Übliche Summenformeln	$\sum^n_{k=1}k=\frac{n(n+1)}2$ $\sum^n_{k=1}k^2=\frac{n(n+1)(2n+1)}6$
Polynomfunktion	$f(x)=a_n\cdot x^n+a_{n-1}\cdot x^{n-1}+..+a_1\cdot x + a_0$
Komposition	$(g\circ f)(2)=g(f(2))$
Funktion	Mapt vom Definitionsbereich $D$ zum Wertebereich $W$
Mitternachtsformel	$D=b^2-4ac$ und $x=\frac{-b\pm \sqrt D}{2a}$

Ableiten

Name	Formel
	$x^k=k\cdot x^{k-1}$
Faktorregel	$(c\cdot f)'(x)=c\cdot f'(x)$
Summenregel	$(f+g)'(x)=f'(x)+g'(x)$
Produktregel	$(u\cdot v)'(x)=u'(x)\cdot v(x)+u(x)\cdot v'(x)$
Quotientenregel	$(\frac u v)'(x)=\frac{u'(x)\cdot v(x)-u(x)\cdot v'(x)}{v(x)^2}$
Kettenregel	$(F\circ u)'(x)=F'(x)\cdot u'(x)$
sin	$sin(x)'=cos(x)$
cos	$cos(x)'=-sin(x)$
$e^x$	$(e^x)'=e^x$
$(a^x)'$	$(a^x)'=a^x\cdot \ln(a)$
$\ln(x)'$	$\ln(x)'=\frac 1 x$
$\log_a(x)'$	$\log_a(x)'=\frac 1 {x\cdot \ln(a)}$
Funktionsgleichung für Tangente	$y(x)=f'(x_0)\cdot (x-x_0)+f(x_0)$

Achtung: Nicht jede Funktion ist differenzierbar. Die Ableitung einer Funktion darf keine plötzliche Sprünge machen

Newton Verfahren

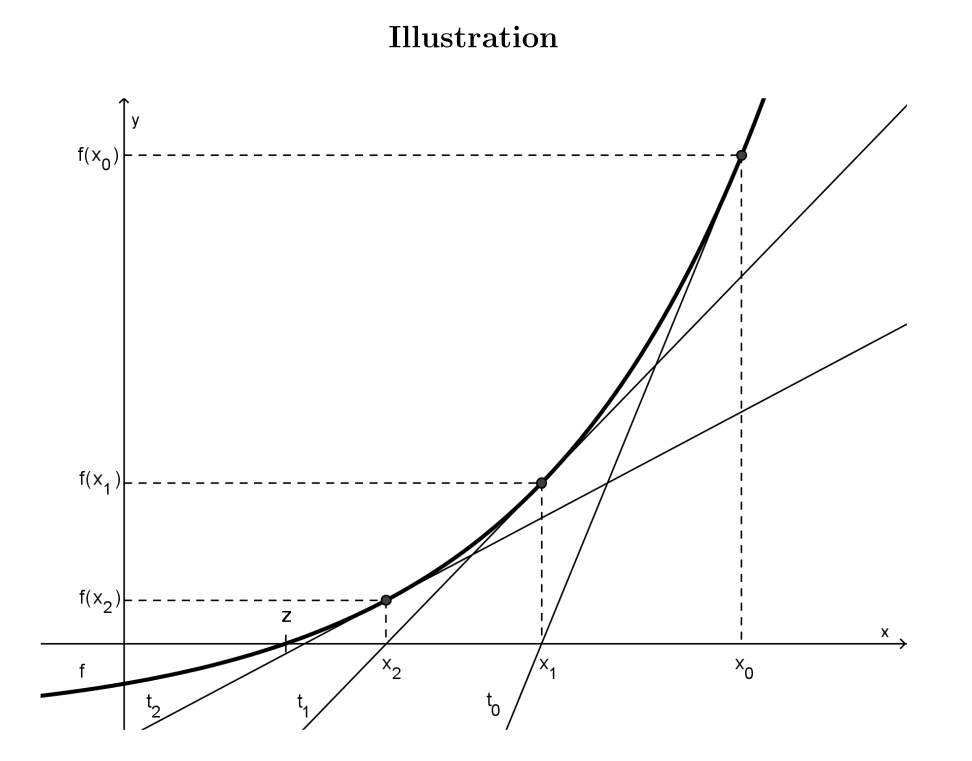
$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$

Integrieren

Ableiten: $a\cdot x^n\rightarrow \frac{a}{n+1}\cdot x^{n+1}$

Schreibweise von Integral von der Fläche zwischen $[a;b]$: $\int^b_a f(x) \mathrm d x =F(b)-F(a)$$

$\int a^x \mathrm d x =\frac {a^x}{\ln(a)} + C$
$\int \ln(x)\mathrm dx=x\cdot \ln(x)-x + C$
$\int \log_a(x)\mathrm dx=\frac 1 {\ln(a)}\cdot (x \cdot \ln(x) -x) + C$
$\int \sin(x)\mathrm dx=-\cos(x)+C$
$\int \cos(x)\mathrm dx=\sin(x)+C$
$\int \tan(x)\mathrm dx = -\ln |\cos(x)|+C$
$\int u^{-1}\mathrm dx=\ln(|u|)$

Reihen & Folgen

Name	explizite Darstellung	implizite Darstellung	aufzählende Darstellung
Arithmetische Folge	$a_n=c+(n-1)\cdot d$	$a_1=c\\a_{n+1}=a_n+d$	$c,c+d,c+2d,c+3d,...$
Geometrische Folge	$a_n=c\cdot q^{n-1}$	$a_1=c\\a_{n+1}=q\cdot a_n$	$c, c\cdot q, c\cdot q^2, c\cdot q^3, ...$
Harmonische Folge	$a_n=\frac 1 n$	(nicht üblich)	$1, \frac 1 2, \frac 1 3, \frac 1 4, ...$
Fibonacci-Folge	(nicht elementar)	$a_1=1, a_2=1\\a_{n+1}=a_n+a_{n+1}$	$1, 1, 2, 3, 5, 8, ...$

Arithmetische Reihee
$a_k=a_1+(k-1)\cdot d$
$s_n=n\cdot a_1+\frac{n(n-1)}2 \cdot d$
$\sum^n_{k=0}(k^2)=\frac{n(n+1)(2n+1)}{6}$
$\sum^n_{k=0}k=\frac{n(n+1)}{2}$
Strebt immer geben $\infty$ oder $-\infty$
Geometrische Reihe
$a_n=q^{(k-1)}\cdot a_1$
$s_n=\frac{a_1(q^n-1)}{q-1}$
Wenn $|q|<1$ ist, dann ist der Grenzwert $\frac {a_1}{1-q}$

Grenzwert

$\lim_{n\to\infty}(c\cdot a_n)=c\cdot \lim_{n\to \infty} a_n$
$\lim_{n\to \infty}(a_n+b_n)=\lim_{n\to \infty}=\lim_{n\to \infty}a_n + \lim_{n\to \infty} b_n$
$\lim_{n\to \infty}(a_b\cdot b_n)=\lim_{n\to \infty}a_b \cdot \lim_{n\to \infty} b_n$
$\lim_{n\to \infty}(\frac {a_n} {b_n})=\lim_{n\to \infty} a_n : \lim_{n\to \infty}b_n$
$\lim_{n\to\infty}(\sqrt a - \sqrt b)=\lim_{n\to\infty}(\frac{(\sqrt a-\sqrt b)(\sqrt a + \sqrt b)}{\sqrt a + \sqrt b})=\lim_{n\to\infty}(\frac{a-b}{\sqrt a + \sqrt b})$

Wenn man einen Bruch in einem $\lim$ hat, dann kann mit dem höchsten $n^k$ mit dem höchsten $k$ gekürzt werden

Beispiel: $$ \lim_{n\to \infty}=\frac{3n^2+7n-3}{n^2+4n-11}=\lim_{n\to \infty}\frac{n^2(3+\frac 7 n-\frac 3 {n^2})}{n^2(1+\frac 4 n - \frac {11} {n^2})}\rightarrow\frac {3+0+0}{1+0+0}=\frac 3 1 = 3 $$

Spezialfall: $\lim_{n\to\infty}(1+\frac 1 n)^n=e=2.718$ $$ \text{Speziallfall: }\lim_{n\to\infty}(1+\frac 1 n)^n=e=2.718\ \text{Beispiel: } \lim_{n\to\infty}(1+\frac{9}{4n})^{-5n}\ (1+\frac{9}{4n})^{-5n}=(1+\frac{9}{4n}\cdot\frac{\frac 1 9}{\frac 1 9})^{-5n}=(1+\frac 1 {\frac {4n} 9})^{-5n}\=(1+\frac 1 {\frac {4n} 9})^{-5n\cdot\frac{\frac{4n} 9}{\frac{4n} 9}}=(1+\frac 1 {\frac {4n} 9})^{\frac{4n} 9\cdot \frac{-5n}{\frac{4n} 9}}=(1+\frac 1 {\frac {4n} 9})^{\frac {4n} 9\cdot \frac{-45} 4}\=((1+\frac 1 {\frac {4n} 9})^{\frac{4n} 9})^{\frac{-45} 4}=e^{\frac{-45} 4} $$

Typ	Funktionswert	Beispiel
Typ 1: Hebbare Definitionslücke Das Zähler- und Nennerpolynom haben dieselbe Nullstelle. Diese kann gekürzt werden	Strebt gegen den gekürzten Bruch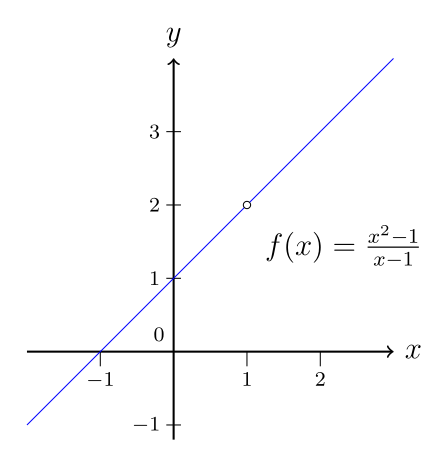
Typ 2: Polstelle Nur das Nennerpolynom hat die Nullstelle. Dies kann nicht gekürzt werden	Strebt gegen $\infty$ oder $-\infty$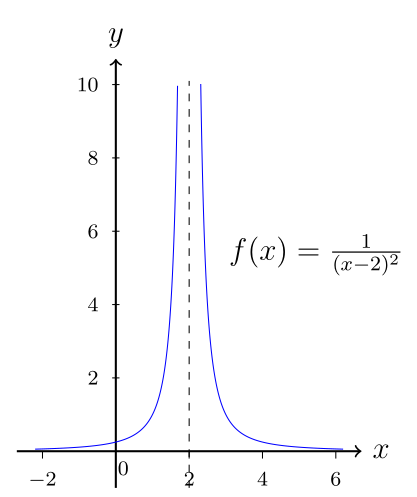

Stetigkeit

Eine Funktion ist stetig, wenn man sie zeichnen kann, ohne den Stift abzusetetzen. Eine stetige Funktion hat keine Sprünge in der ersten Ableitung und keine Sprünge in der eigentlichen Funktion.

Nullstellen finden mit Stetigkeit

Zwei Punkte, bei denen der Y-Wert ein verschiedenes Vorzeichen hat
Den Mittelwert zischen den Punkten bilden
Zu 1. gehen, aber diesem mit dem Mittelpunkt als Punkt, so dass die zwei Pünkte ein verschiedenes Vorzeichen haben

Hornerschema

Die Werte ($b_n$), welche unter dem Strich stehen, sind die Koeffizenten für das $q(x)$ in $f(x)=(x-x_0)\cdot q(x)$. In diesem fall also $q(x)=3x^3-8x^2+21x-49$. Dafür muss das Resultat/Rest 0 sein!

Polynomdivision

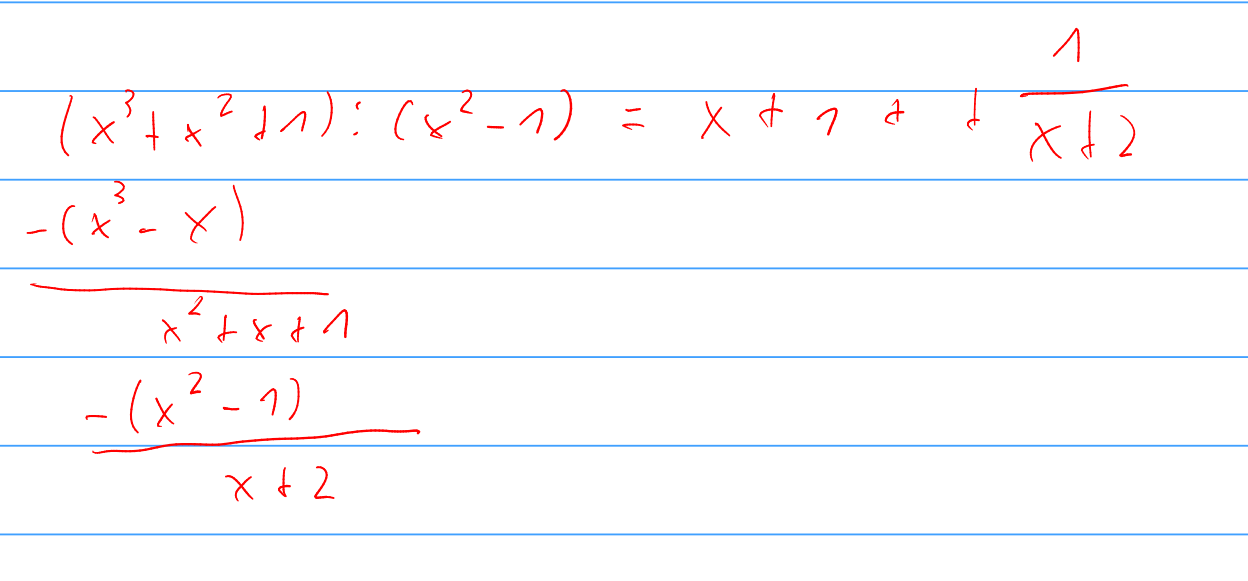
Extremwerte

1. Ableitung	2. Ableitung	Beschreibung
$f'(x)>0$	$f''(x_0)>0$	$f$ macht eine Linkskurve nach oben bei $(x_0, y_0)$
$f'(x)>0$	$f''(x_0)<0$	$f$ macht eine Rechtskurve nach oben bei $(x_0, y_0)$
$f'(x)<0$	$f''(x_0)>0$	$f$ nmacht eine Linkskurve nach unten bei $(x_0, y_0)$
$f'(x)<0$	$f''(x_0)<0$	$f$ macht eine Rechtskurve nach unten bei $(x_0, y_0)$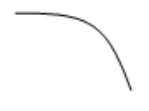
$f'(x)=0$	$f''(x)<0$	$f$ hat ein lokales Maximum bei $(x_0, y_0)$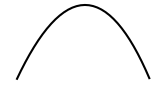
$f'(x)=0$	$f''(x)>0$	$f$ hat ein lokales Minimum bei $(x_0, y_0)$

	$x_0$ heisst	$f(x_0)$ heisst	$(x_0, y_0)$ heisst
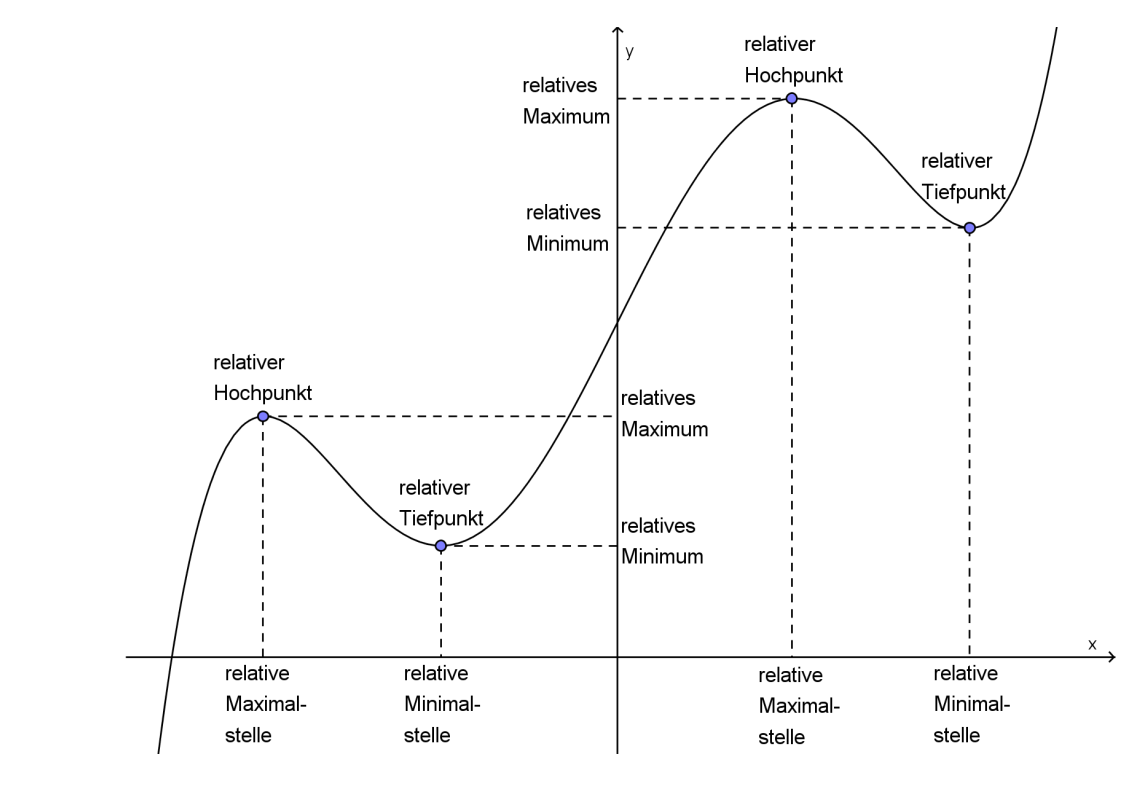
Maxiumum	(relative) Maximalstelle	(relatives) Maximum/Maximalwert	(relativer) Hochpunkt
Minimum	(relative) Minimalstelle	(relatives) Minimum/Minimalwert	(relativer) Tiefpunkt
Oberbegriff	(relative) Extremalstelle	(relatives) Extremum/Extremalwert	(relativer) Extremalpunkt

Wendepunkte und Sattelpunkte

Eine Wendepunkt, ist wenn eine Rechtskurve in eine Linkskurve, oder umgekehrt, geht. Ein Spezialfall ist es, wenn $f'(x)=0$ ist, dann spricht man von einem Sattelpunkt.

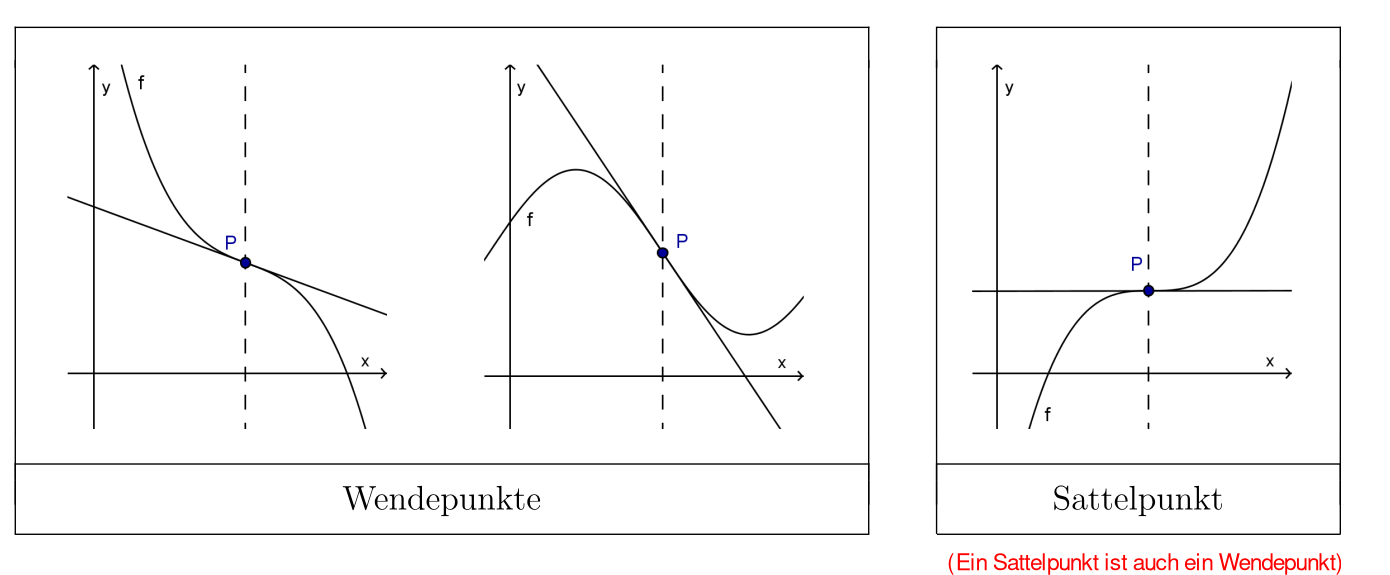
Wenn $f''(x_0)=0$ und $f'''(x_0)\neq 0$ ist, dann ist es sicherlich einen Wendepunkt.

Wenn zusätzlich noch $f'(x_0)=0$ gilt, dann ist es ein Sattelpunkt

Fragen für die Kurvendiskussion

Definitionsbereich?
Symmetrieeigenschaften (gerade/ungerade), Periode?
Schnittpunkte mit Achsen, Polstellen?
Randpunkte, bzw. Verhalten, wenn $x$ gegen die Grenzen des Definitionsbereichs strebt?
Kandidaten für Extrema bestimmen und untersuchen
Wendepunkte suchen
Tabelle von Werten aufstellen (falls noch nötig)

Extremaufgaben

Zielgrösse identifizieren
Unabhängige Variable identifizieren
Definitionsbereich bestimmen
Zielgrösse als Funktion mit unabhängigen Variabeln als Argument ausdrücken
Relative Maxima/Minima bestimmen; Randpunkte auch berürcksichtigen!
Welche relative Extrema sind auch absolute?

Name	Formel
	\(x^k=k\cdot x^{k-1}\)
Faktorregel	\((c\cdot f)'(x)=c\cdot f'(x)\)
Summenregel	\((f+g)'(x)=f'(x)+g'(x)\)
Produktregel	\((u\cdot v)'(x)=u'(x)\cdot v(x)+u(x)\cdot v'(x)\)
Quotientenregel	\((\frac u v)'(x)=\frac{u'(x)\cdot v(x)-u(x)\cdot v'(x)}{v(x)^2}\)
Kettenregel	\((F\circ u)'(x)=F'(x)\cdot u'(x)\)
sin	\(sin(x)'=cos(x)\)
cos	\(cos(x)'=-sin(x)\)
\(e^x\)	\((e^x)'=e^x\)
\((a^x)'\)	\((a^x)'=a^x\cdot \ln(a)\)
\(\ln(x)'\)	\(\ln(x)'=\frac 1 x\)
\(\log_a(x)'\)	\(\log_a(x)'=\frac 1 {x\cdot \ln(a)}\)
Funktionsgleichung für Tangente	\(y(x)=f'(x_0)\cdot (x-x_0)+f(x_0)\)

1. Ableitung	2. Ableitung	Beschreibung
\(f'(x)>0\)	\(f''(x_0)>0\)	\(f\) macht eine Linkskurve nach oben bei \((x_0, y_0)\)
\(f'(x)>0\)	\(f''(x_0)<0\)	\(f\) macht eine Rechtskurve nach oben bei \((x_0, y_0)\)
\(f'(x)<0\)	\(f''(x_0)>0\)	\(f\) nmacht eine Linkskurve nach unten bei \((x_0, y_0)\)
\(f'(x)<0\)	\(f''(x_0)<0\)	\(f\) macht eine Rechtskurve nach unten bei \((x_0, y_0)\)
\(f'(x)=0\)	\(f''(x)<0\)	\(f\) hat ein lokales Maximum bei \((x_0, y_0)\)
\(f'(x)=0\)	\(f''(x)>0\)	\(f\) hat ein lokales Minimum bei \((x_0, y_0)\)

Name	explizite Darstellung	implizite Darstellung	aufzählende Darstellung
Arithmetische Folge	\(a_n=c+(n-1)\cdot d\)	\(a_1=c\\a_{n+1}=a_n+d\)	\(c,c+d,c+2d,c+3d,...\)
Geometrische Folge	\(a_n=c\cdot q^{n-1}\)	\(a_1=c\\a_{n+1}=q\cdot a_n\)	\(c, c\cdot q, c\cdot q^2, c\cdot q^3, ...\)
Harmonische Folge	\(a_n=\frac 1 n\)	(nicht üblich)	\(1, \frac 1 2, \frac 1 3, \frac 1 4, ...\)
Fibonacci-Folge	(nicht elementar)	\(a_1=1, a_2=1\\a_{n+1}=a_n+a_{n+1}\)	\(1, 1, 2, 3, 5, 8, ...\)