ADS
Abstrakter Datentyp
Jede Klasse besteht aus einer sichtbarer Schnittstelle und eine von Aussen, unsichtbare Implementation.
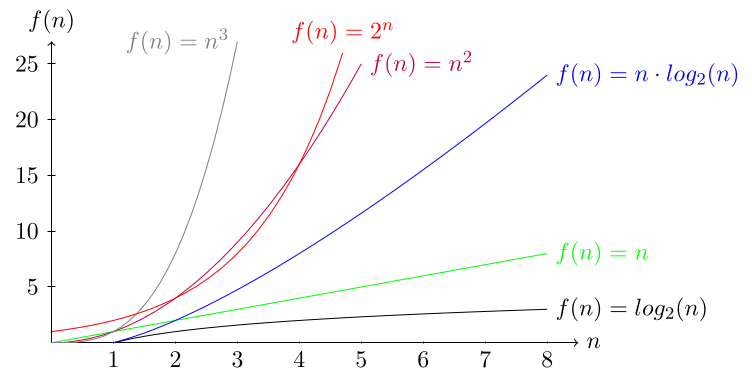
Big-O Notation
Es existiert ein \(n_0\in \N\) und ein \(c\in \N\), so dass für alle \(n\ge n_o\) gilt: \(f(n) \le c\cdot g(n)\).
Es gibt einige spezielle Rechenregel zu der Big-O Notation:
- Konstante Vorfaktoren können ignoriert werden (dafür gibt es das \(c\))
- Bei einem Polygon ist nur die höchste Potenz entscheidend
Rechenregeln:
- \(O(f\cdot g) = O(f)\cdot O(g)\) (wobei \(f\) und \(g\) Funktionen sind)
- \(O(r\cdot f)=O(f)\) (wobei \(r\) eine Konstante ist)
- \(O(f+g)=O(f)\), wenn \(f >g\) gilt
Beispiele:
- \(O(1)\): konstanter Aufwand
- \(O(\log n)\): logarithmischer Aufwand
- \(O(n)\): linearer Aufwand
- \(O(n\cdot \log n)\): linear-logarithmischer Aufwand
- \(O(n^2)\): quadratischer Aufwand
- \(O(n^k), k>1\): polynomialer Aufwand
- \(O(k^n)\): exponentieller Aufwand
- \(O(n!)\): faktorieller Aufwand
Invarianten, Vor- und Nachbedingungen
Invariante sind Aussagen, welche über die Ausführung hinweg korrekt bleiben.
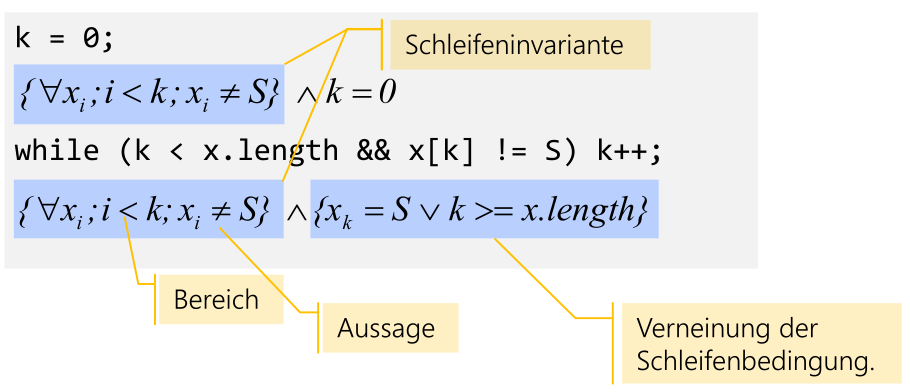
Vorbedingungen ist eine Aussage, welche vor dem Ausführen einer Programmsequenz gilt. Nachbedingungen sind Aussagen, welche nach dem Ausführen einer Programmsequenz gilt.

Algorithmus
Ein Algorithmus ist eine Anleitung zur Lösung einer Aufgabenstellung, die so präzise formuliert ist, dass sie “mechanisch” ausgeführt werden kann.
Eigenschaft:
-
Determinierheit: Identische Eingaben führen zur selben Ausgabe
-
Determinismus: Ablauf des Verfahrens ist an jedem Punkt fest vorgeschrieben (keine Wahlfreiheit)
-
Terminierung: Für jede Eigenschaft liegt das Ergebnis nach endlich vielen Schritten vor
-
Effizienz: Wie wirdschaftlich der Algorithmus ist