Numerische Itegration
Rechteck- & Trapezregel
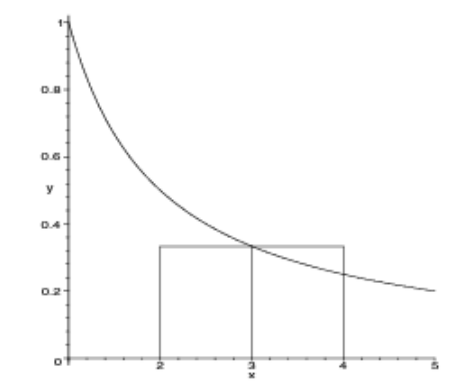
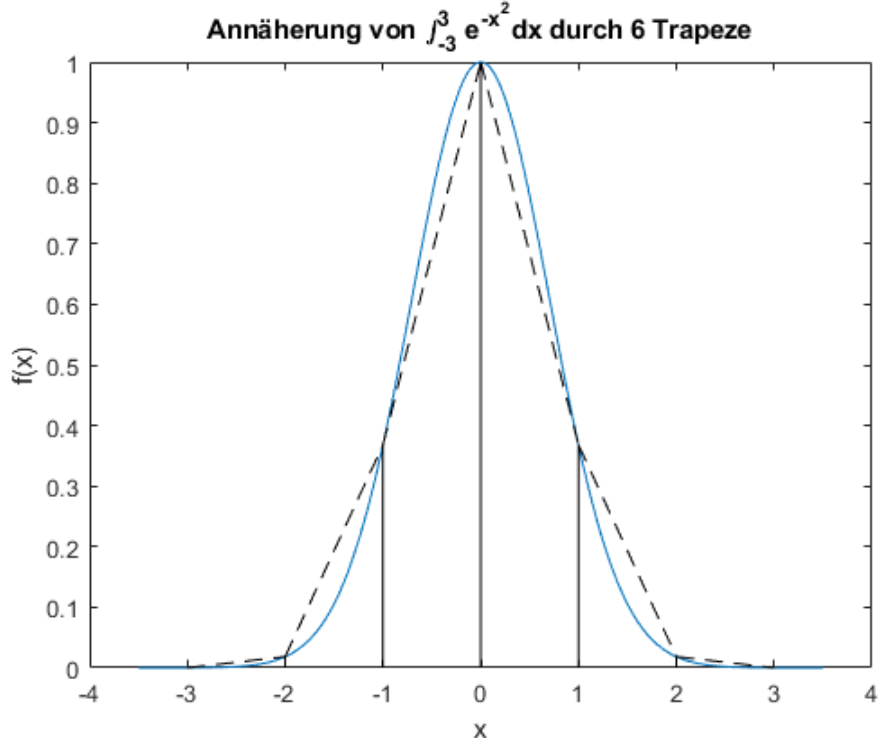
Die folgenden formel ziehen ein Rechteck, bzw. Trapez über das ganze Integral.
$$ \text{Das Integral}\ \int_a^b f(x)\mathrm d x\ \ \text{kann folgendermassen approximiert werden}\ Rf=f\left(\frac{a+b}{2}\right) \cdot (b - a)\ Tf=\frac{f(a) + f(b)} 2 \cdot (b - a) $$ (Rf = Rechtecksregel, Tf = Trapezregel)
Für die summierte Rechteck- & Trapezregel wird das Integral in kleinere Schritte mit der breite \(h\) unterteilt.
$$
Rf(h)=h\cdot \sum^{n-1}{i=0} f(x_i +\frac h 2)\
Tf(h)=h\cdot \left(\frac{f(a) + f(b)}{2} +\sum^{n-1} f(x_i) \right)\
\text{wobei gilt}
x_i=a+i\cdot h\
h=\frac{b-a} n
$$
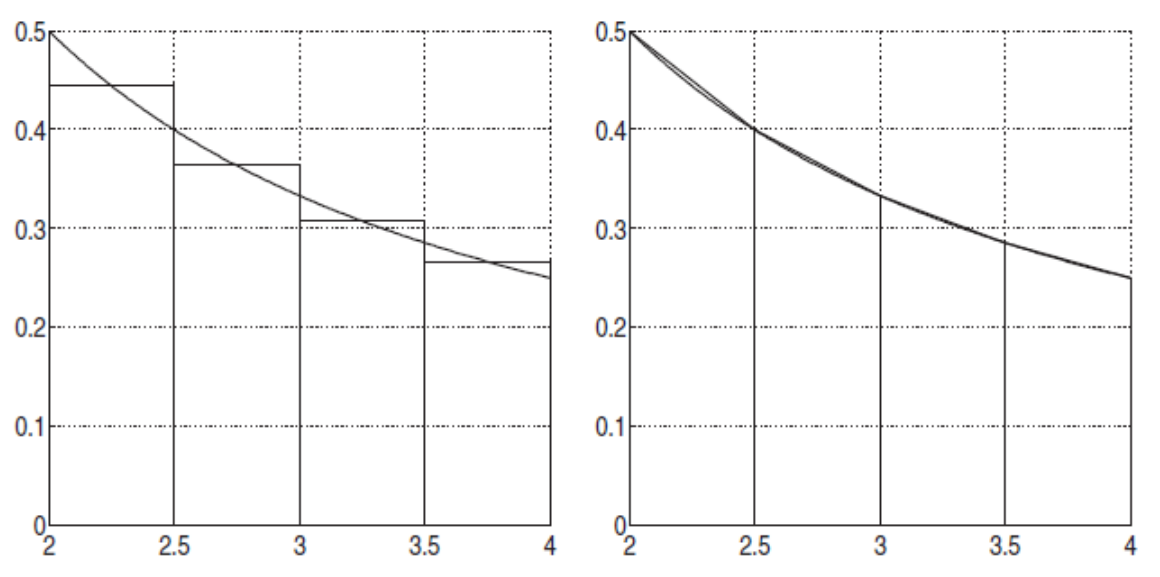
Simpsonregel
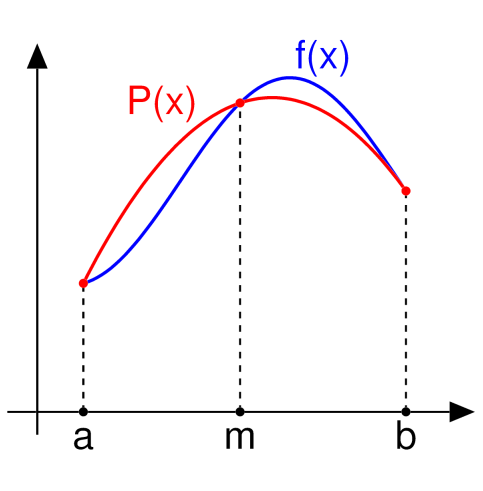
Für das lösen eines Segments müssen folgende Formel ausgerechnet werden. Dabei wird das Polynom \(p(x)=\alpha+\beta(x-a) + \gamma(x-a)(x-b)\) verwendet.
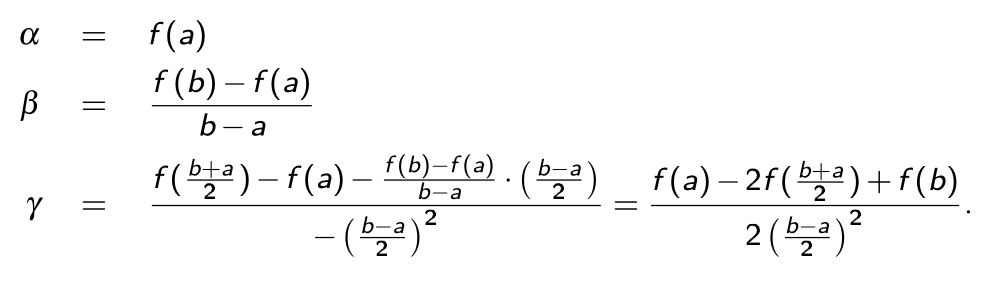
Da \(f(x)\approx p(x)\) gilt, kann das Polynom integriert werden:
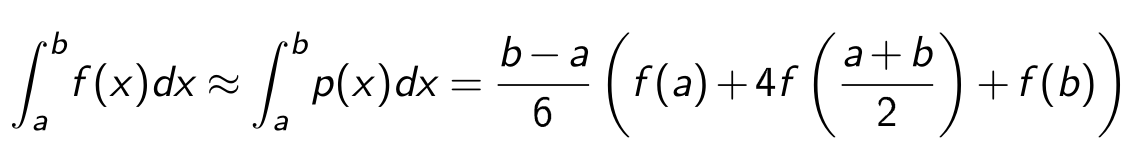
Die Regel oben haben nur ein Segment benutzt. Wie aber auch bei der Rechtecks- und Trapezregel, kann auch hier die summierte Simpsonregel verwendet werden. $$ Sf(h)=\frac h 3 \left(\frac 1 2 f(a) + \sum^{n-1}{i=1} f(x_i) + 2 \sum^n \right) + \frac 1 2 f(b) \right) $$ Die Simpsonsregel kann auch mit dem Rechtecks- und Trapezregel berechnet werden: $$ Sf(h)=\frac 1 3 (Tf(h) + 2 Rf(h)) $$} f\left (\frac{x_{i-1}+x_i}{2
Fehlerabschätzung
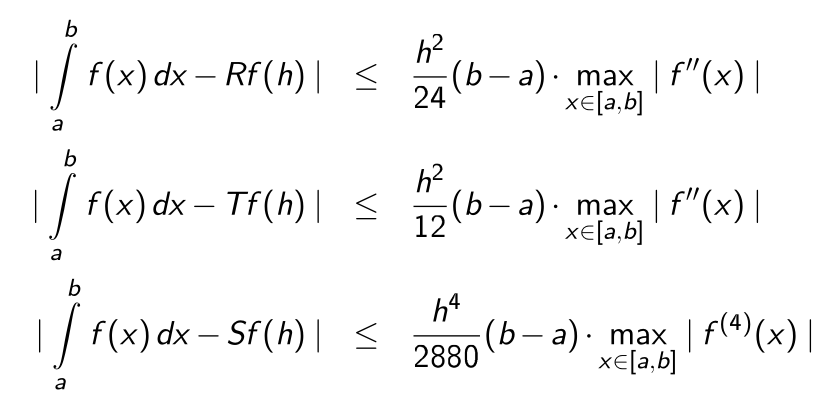
Gaussformel
Die folgenden Formel bestimmen das Integral zwischen \(a\) und \(b\), wenn es \(n\) Stützpunkte gibt. Dabei müssen die Stützpunkte nicht äquidistant sein.
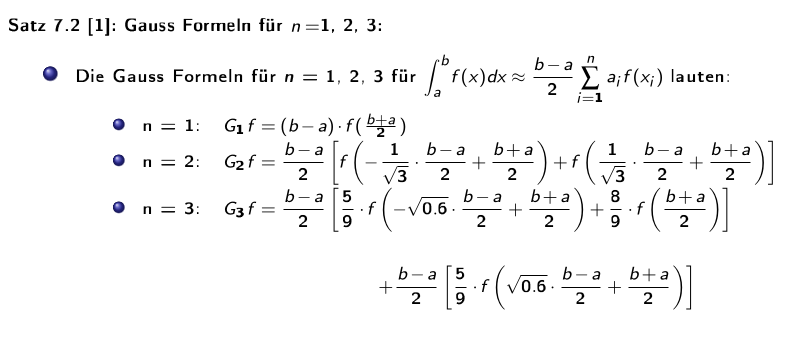
Romberg Extrapolation

Die Rekursion wird ausgerechnet bis \(k=0\) wird, da dann die Formel \(T_{j0}=Tf\left(\frac{b-a}{2^j}\right)\)
Da die Werte von \(f(...)\) immer in \(T_{j0}\) wiederverwendet werden, kann dies mit der folgenden Formel vereinfacht werden: $$ T_{j0}=\frac 1 2 T_{j-1,0}+h_j\sum^{n_{j-1}}_{i=1}f(a+(2i-1)h_j) $$ Die zweite Spalte \(T_{j1}\) kann mit der Simpson-Regel berechnet werden: $$
$$
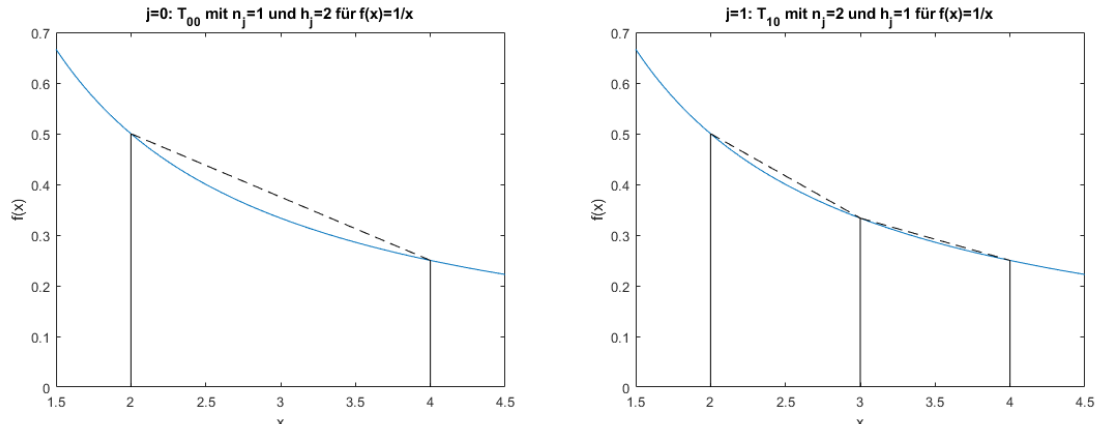
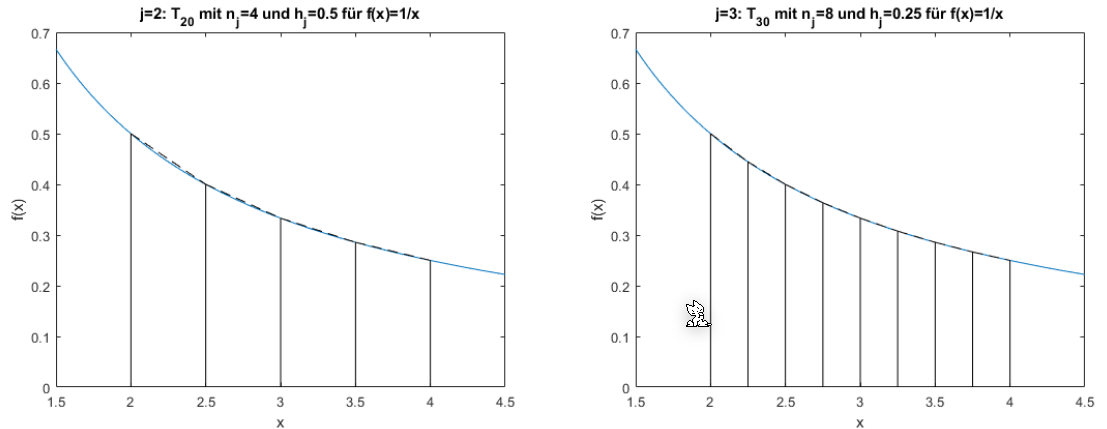
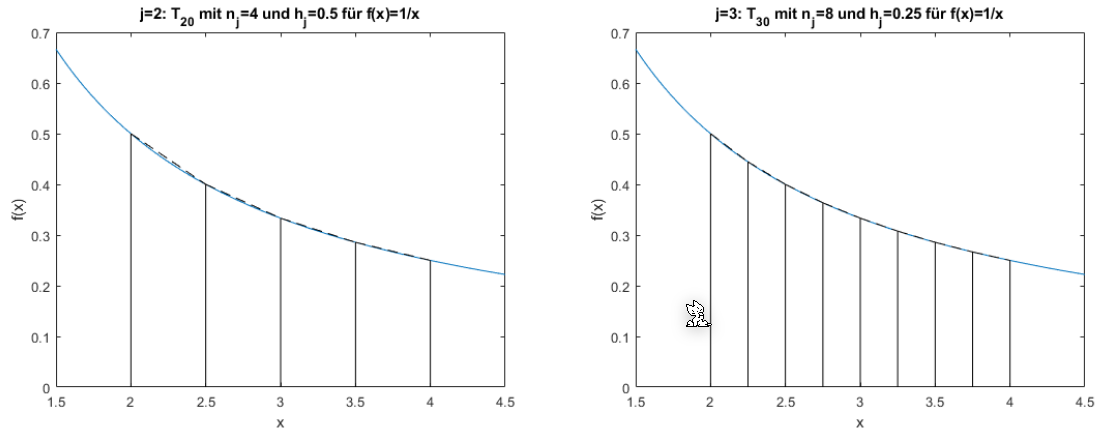
Die folgende Graphik zeigt die oben abgebildete Rekursion:
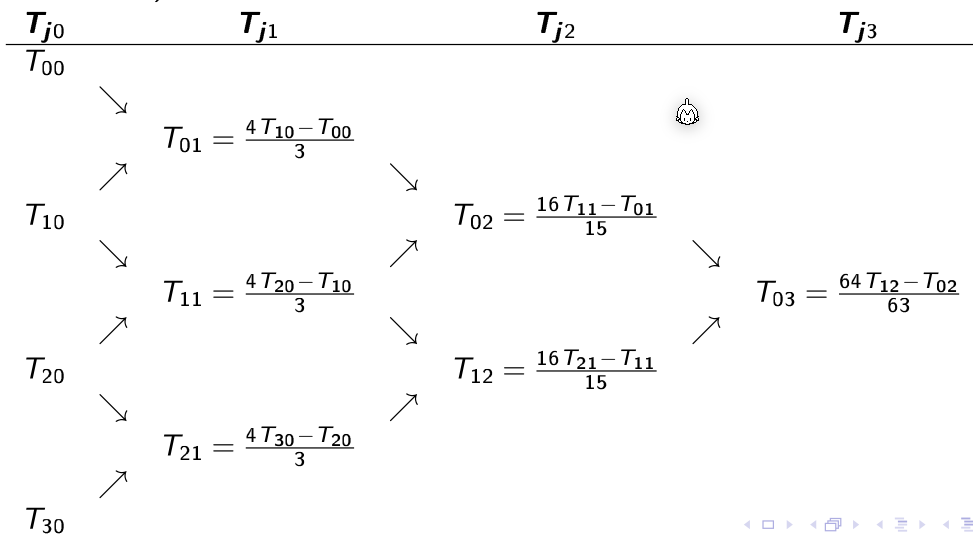
Die folgenden zwei Graphen zeigen \(T_{00}\) und \(T_{10}\). Wenn \(j\) um 1 höher wird, wird die X-Achse halbiert. Dasselbe gilt für \(T_{30}\) und \(T_{40}\)