Support Vector Machine (SVM)
A side node: the negative label is usually \(-1\), and the positive label is usually \(1\) for mathematical reasons.
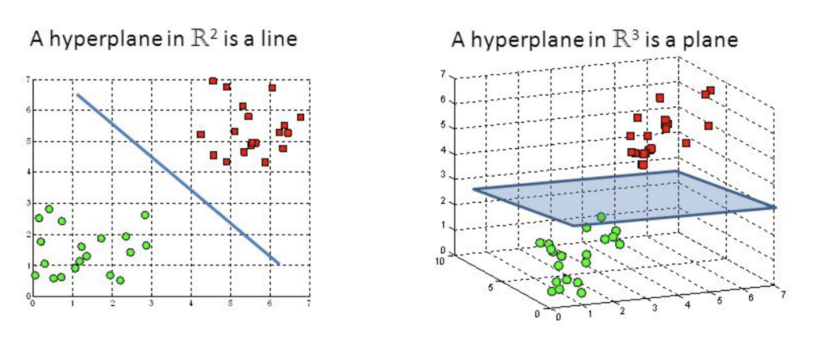
A SVM categorises data points by drawing a hyperplane. A hyperplane is a line in 2d or a plane in 3d.
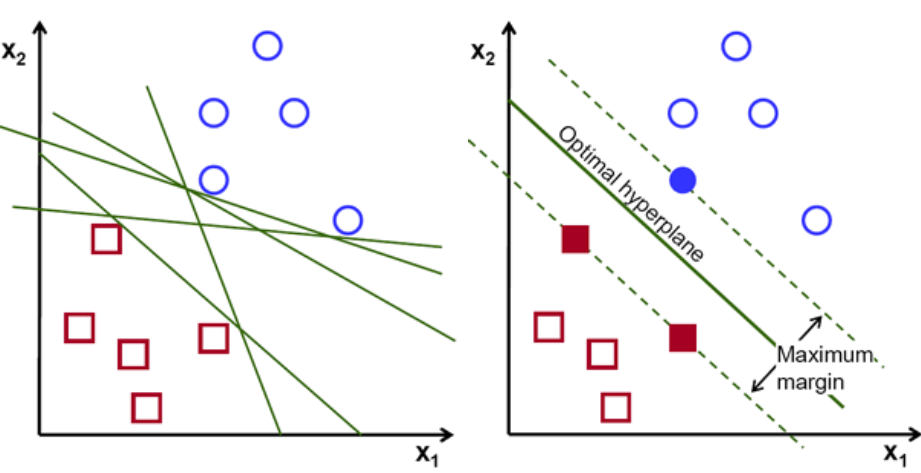
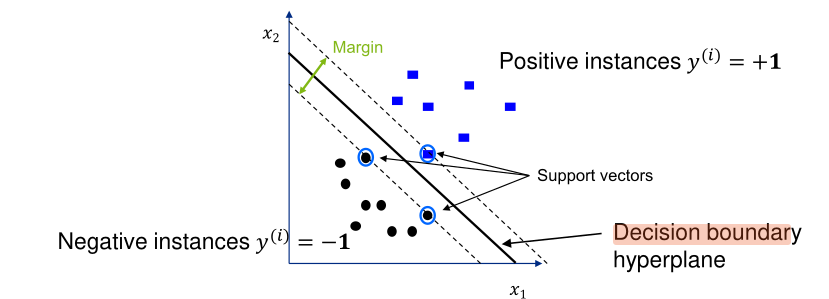
The goal of the SVM is to maximise for the margin between points:
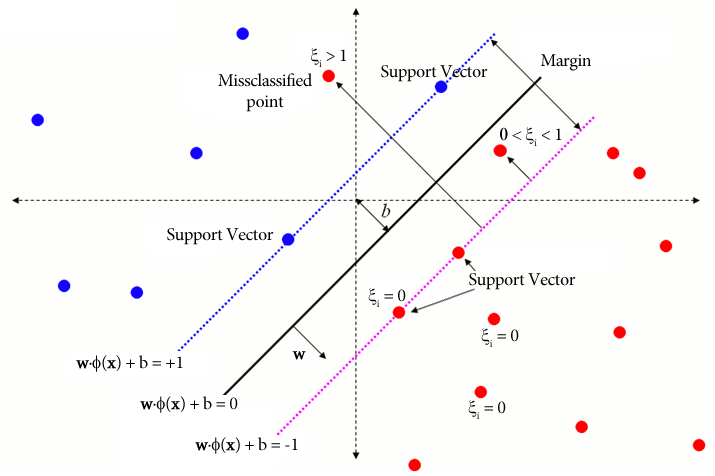
The following explains all the variables associated with SVM:
Width of Margin
With the following formula, one can calculate the distance between two hyperplanes.

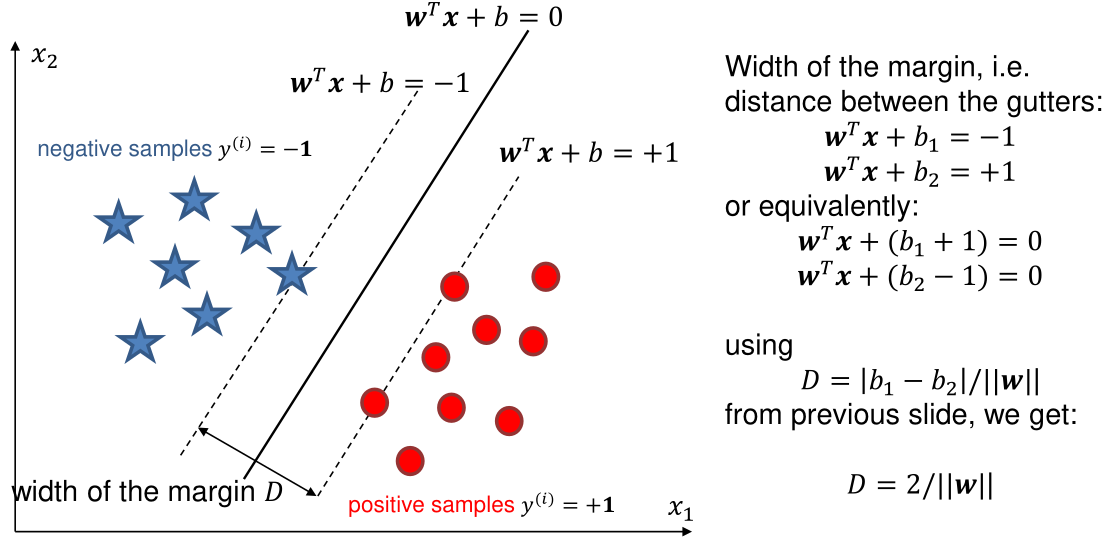
(Correction: \(b_1=b_2\); The subscript is incorrect)
Additionally, every sample needs to be on correct side of the hyperplane. This condition is encoded in the following inequations:
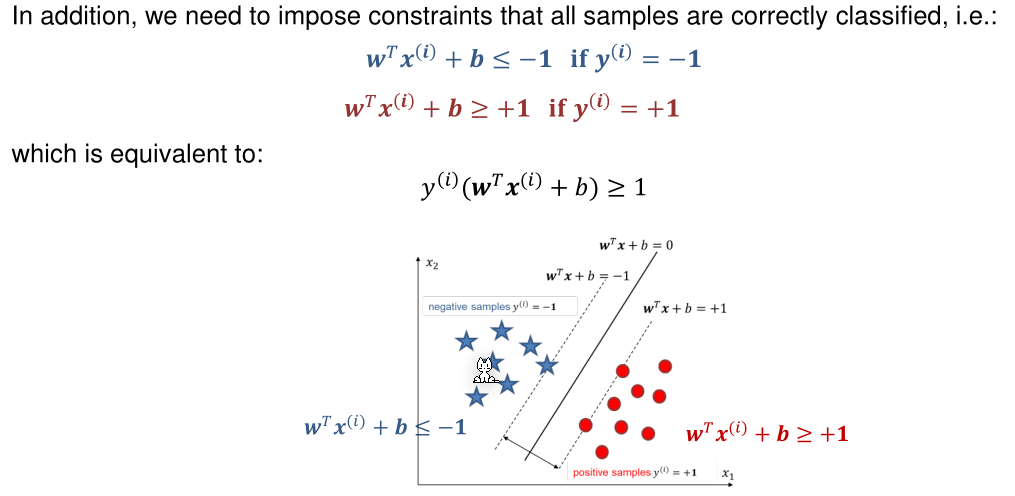
Optimisation Problem
SVM optimise for the widest margin \(D=\frac{2}{||w||}\). This is equivalent to minimising \(||w||\) or \(\frac 1 2 ||w||^2\).
Soft-Margin SVMs
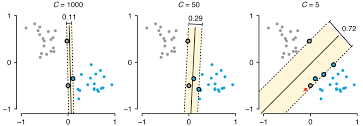
Training samples can be mislabelled or noise. To deal with this, we can allow some samples to be on the "wrong" side, with a penalty, to archive a wider margin.
The parameter \(C\) controls what the penalty of miss-classification is. A large \(C\) would result in almost no miss-classified points and a small \(C\) would result in a large amount of miss-classified points.
The following explains all the variables associated with SVM:

In the cost function every miss-classified sample is summed: $$ \frac 1 2 ||w||^2 + C \sum^m_{i=1}\xi_i\ y_i(w^Tx_i+b)\ge 1 - \xi_i $$ \(\xi\) expresses how much a sample is missclassified. If \(\xi \in ]1;\infty[\), then the sample is on the wrong side and missclassified. If \(\xi \in ]0; 1]\), then the sample is in the margin and is a margin If \(\xi = 0\), then the sample is on the correct side.
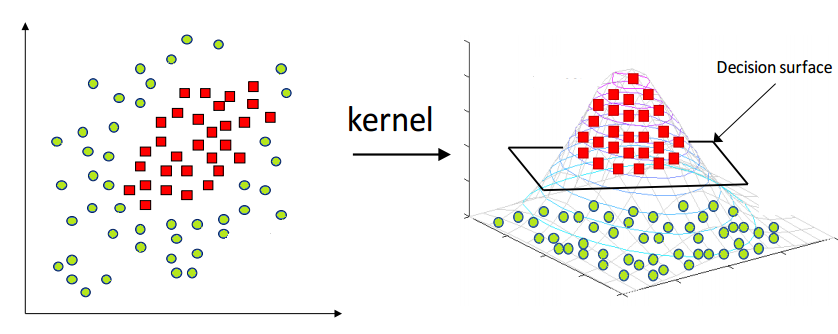
Kernel Trick
Sometimes data can't be separated by a hyperplane. In those cases an additional dimension can be added with a mapping function (e.g. \(z = x^2 + y^2\)).
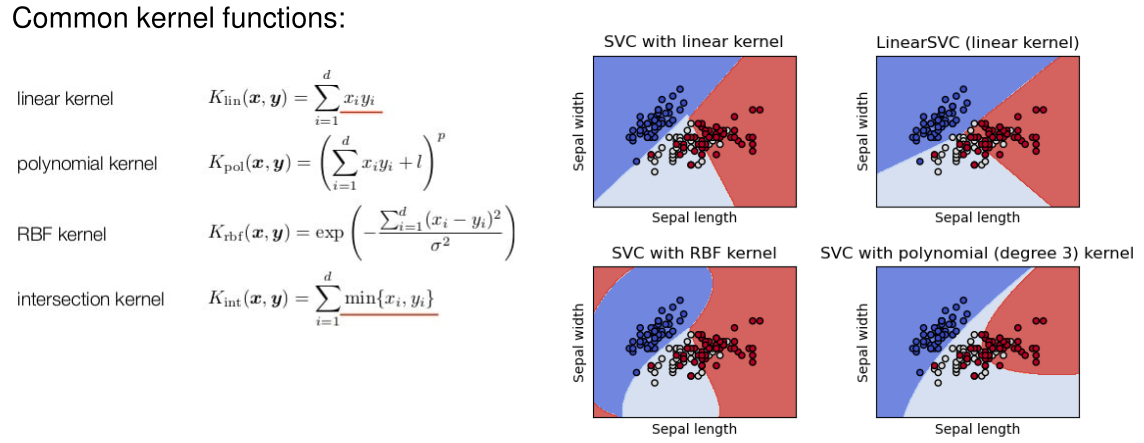
The following functions are common kernel functions:
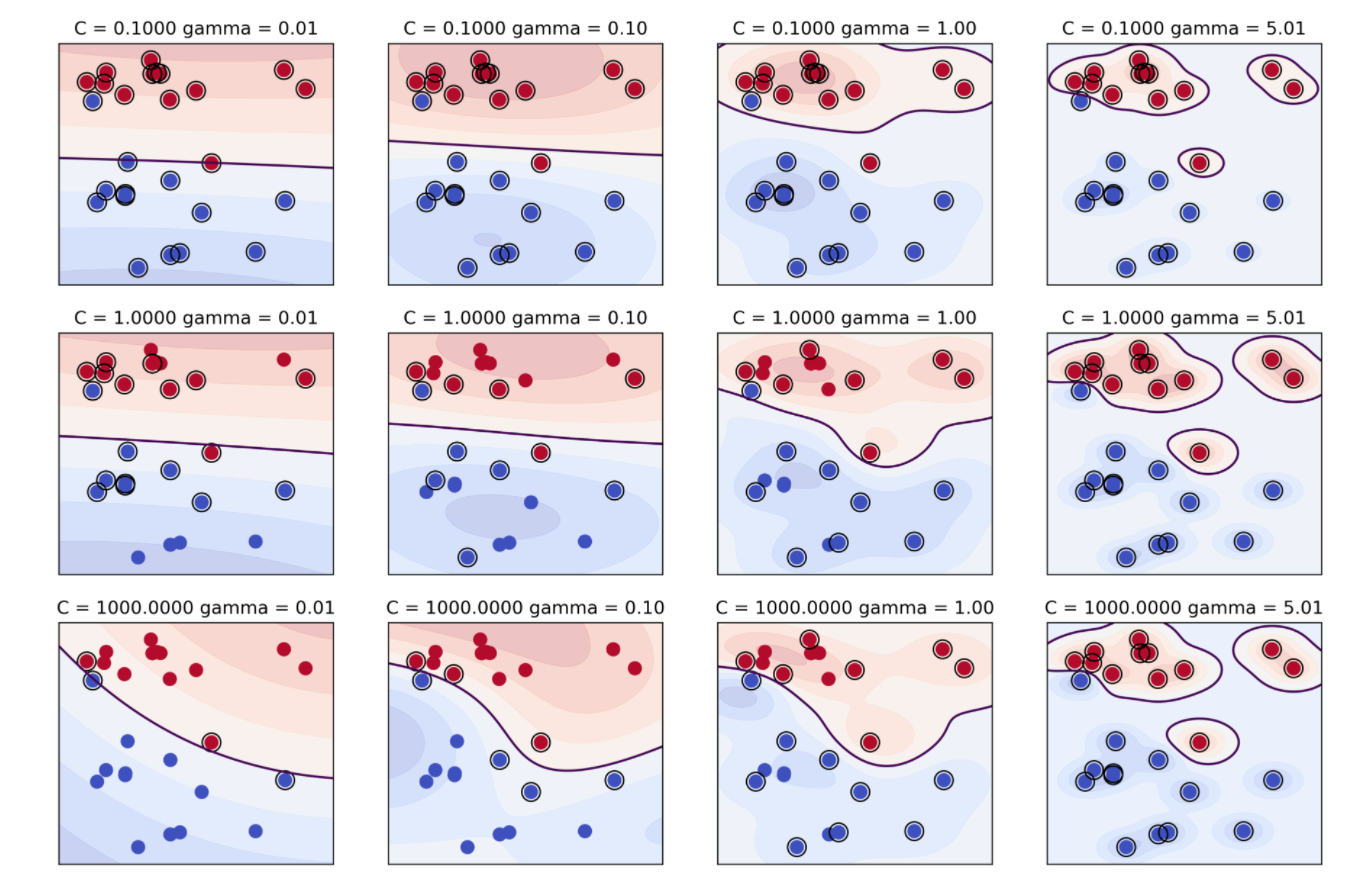
RBF-Kernel
If \(\gamma\) is small, then the variance \(\sigma\) gets large and support vectors "see" far. If \(\gamma\) is big, then the variance \(\sigma\) becomes small and the support vectors "see" only a short distance. \(\gamma\) can also be seen to influence how flexible the model is. The bigger it is, the more flexible the model is.
Multi-Class
One vs Rest
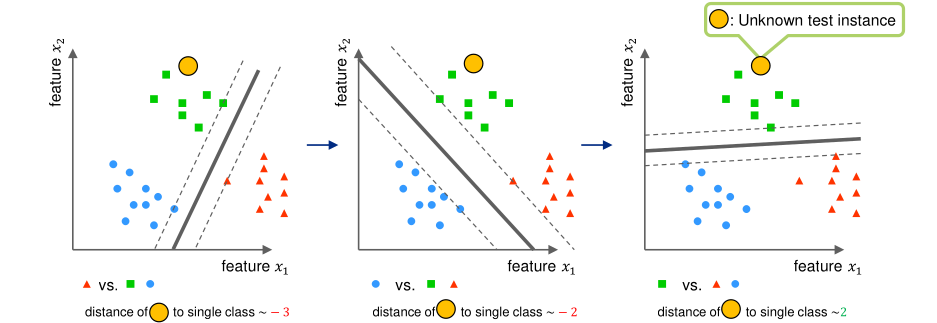
For every class, the margin for the class against all other classes is calculated.
One vs One
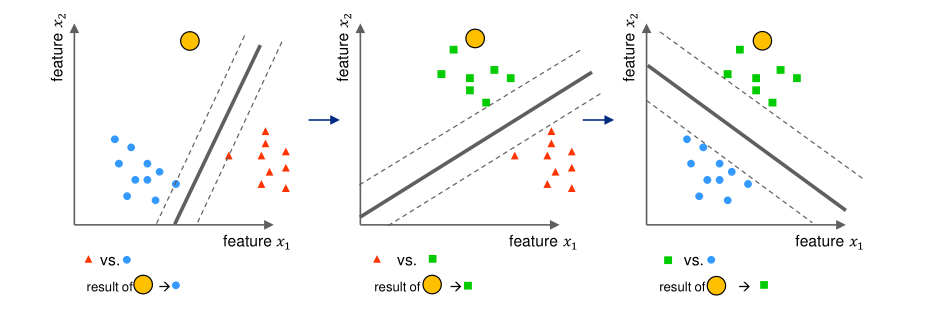
A margin is created for every combination of two classes.