Rekursive

Jede Rekursion kann in eine iterativen Algorithmus umgewandelt werden.

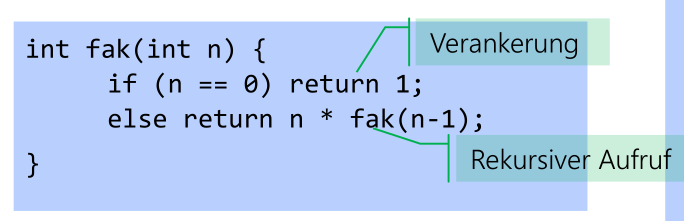
Verankerung: Die Stopp-Bedingungen
Rekursiven-Aufruf: Die Operation, welche zum rekursiven Aufruft führt

Rekursionstiefe

Die Rekursionstiefe ist, wie viele Stackframes es maximal gibt.

Zeitkomplexität und Speicherkapazität

Um die Ordnung von einem rekursiven Algorithmen auszurechnen, kann \(T_{n}\) definiert werden und für jeden Aufruf \(T_{n - 1}\) einsetzen. Danach einige \(T_n\) auflösen und den Trend sehen.

Zeitkomplexität für Türme von Hanoi

void hanoi (int n, char from, char to, char help) {
    if (n > 0) {
        hanoi(n-1, from, help, to);
        System.out.println("bewege " + from + " nach " + to); 
        hanoi(n-1, help, to, from);
    }
}

\[ T_n=T_{n-1}+T_{n-1}=(T_{n-2}+T_{n-2})+(T_{n-2}+T_{n-2})\Rightarrow O(2^n) \]

Indirekte Rekursive

Eine indirekte Rekursive besteht aus zwei Methoden, welche sie sich gegenseitig aufrufen.

public int p(int a) {
    int x = q(a);
}
public int q(int a) {
    int x = p(a - 1);
}

Tail Recursion

Eine Tail Recursion ist eine Rekursion, bei welcher die letzte Expression den rekursive Aufruf ist. Diese können einfach in einen iterativen Algorithmus umgebaut werden.

int fak(int n) {
    if (n == 0) return 1;
    else return n * fak(n - 1);
}

int fak(int n) {
    if (n == 0) return 1;
    else {
        int res = n;
        while(n > 1) {
            n--;
            res = n * res;
        }
        return res;
    }
}