---

tags: - summary - DM title: DM Summary

---

Summary - 2022-01-17

• Summary - 2022-01-17
  • Aussagenlogik
    • Gesetze
    • Beweistechniken
  • Semantik
  • Mengen
  • Relationen
    • Hase Diagram
  • Volständige Induktion
  • Kleinster Verbrecher
  • Teilbarkeit
    • Rechnenregeln ggT
    • (Erweiterten) Euklischer Algorithmus
    • Modulare Arithmethik
    • Eulerische \(\varphi\)-Funktion
    • Chinesischer Restsatz
    • Kleiner Satz von Fermat

Aussagenlogik

Begriff	Erklärung
\(\top\) (Tautologie)	immer wahr
\(\bot\) (Wiederspruch)	immer falsch
\(\vee\)	oder
\(\wedge\)	und

Bindung: \(\neg, \wedge, \vee, \Rightarrow, \Leftrightarrow\)

Gesetze

• Distributivgesetzt: \(A \wedge (B \vee C) \Leftrightarrow (A \wedge B) \vee (A \wedge C)\)
• Der Morgen: \(\neg(A\vee B) \Leftrightarrow \neg A \wedge \neg B\)
• Implikation: \(A \Rightarrow B \Leftrightarrow \neg A \vee B\)
• Kontraposition: \(A \Rightarrow B \Leftrightarrow \neg B \Rightarrow \neg A\)
• Äquivalenz \((A \Leftrightarrow B) \Leftrightarrow (A \Rightarrow B) \wedge (B \Rightarrow A) \Leftrightarrow (\neg A \vee B) \wedge (\neg B \vee A)\)

Formel	Erklärung
\(A(x):=\text{"x ist einfach"}\)	Aussage
\(\neg\exists x\in P A(x)\) oder \(\forall x \in P(\neg A(x))\)	Keine Prüfung ist einfach
\(\exists x \in P A(x) \wedge (\forall y,z\in P(A(x)\wedge A(y)\Rightarrow x=y))\)	Genau eine Prüfung ist einfach
\(\exists x \in P A(x) \wedge (\forall a, b, c \in P (a\neq b \neq c \Rightarrow \neg(A(a) \wedge A(b) \wedge A(c)))\)	Genau zwei Prüfungen sind einfach
\(\exists a,b \in P(a\neq b \wedge A(a) )\)

Beweistechniken

• Direkten Beweis

• So veralgemeinern, dass der einte der Term gleich dem anderen Term ist

• Beweis durch Widerspruch

• Anstatt zu zeigen, dass die Aussage A immer wahr ist, wird bewiessen, dass A niemals falsch ist. Also Anstatt \(\forall n (A(n) \Rightarrow B(n)): true\) soll man beweissen \(\neg (\forall n(A(n)\Rightarrow B(n))):false\) ist

• Beweis durch (Gegen-) Beispiel

• Wenn beweissen werden soll, dass etwas immer korrekt oder immer falsch ist, kann mit ein korrekten, bzw. falschem Beispiel gezeigt werden, dass die Aussage falsch ist

• Beweis durch Kontraposition

• Es gillt die Aussage von der Form \(A \Rightarrow B \Leftrightarrow \neg B \Rightarrow \neg A\)

• Äquivalenz

• Da eine Äquivalenz \((A \Leftrightarrow B) \Leftrightarrow (A \Rightarrow B \wedge B \Rightarrow A)\) ist, kann einfach das zweitere bewiessen werden.

Semantik

Begriff	Erklärung
Gülltig oder Wahr	Bei einer spezifischen Belegung wahr
Allgemeingülltig	Bei allen Belegungen wahr
Erfüllbar	mind. eine Belegung ist erfüllbar
Unerfüllbar	immer falsch
Wiederlegbar	mind. einmal falsch; nicht umbedingt immer falsch
Literale	\(\neg a \text{ oder } a\)
Negotions Normalform (NNF)	Keine Implikationen und alle\(\neg\) in Literale
Disjunktive Normalform (DNF)	Form:\((L_1 \wedge L_2 \wedge ...)\vee (L_3 \wedge L_4) \vee ...\)
Konjuktive Normalform (KNF)	Form:\(L_1 \vee L_2 \vee ...) \wedge (L_3 \vee L_4)\wedge ...\)
Funktional Vollständig	Menge von Logischen Verknüpfungen, welche die Funktionen\(\vee, \wedge, \neg, \rightarrow\) darstellen können

Mengen

Begriff	Erklärung
Natürliche Zahlen (\(\N\))	\([0; \infty]\)
Ganze Zahlen (\(\Z\))	\([-\infty;\infty]\)
Rationale Zahlen (\(\mathbb Q\))	Alle Zahlen, darstellbar durch einen Bruch
Reele Zahlen (\(\R\))	Alle Zahlen mit einem Komma (\(\pi\), \(e\), 2.32, 2, ...)
Intervallschreibweisse	Ist immer im Zahlenbereich \(\R\)
Teilmenge (\(X \subseteq Y\))	\(\forall x (x \in X \Rightarrow x \in Y)\) / X ist eine Teilmenge von Y, X=Y kann auch sein
Echte Teilmenge (\(X \subsetneq Y\))	\(X \subseteq Y \wedge X \neq Y\) / X ist eine Teilmenge von Y, X kann nicht Y sein
Potenzmenge (\(\mathcal P(X)\))	Menge aller Teilmenge (\(\mathcal P(\{0, 1\})=\{\emptyset, \{0\}, \{1\}, \{0, 1\} \}\). Die Mächtigkeit ist \(\mathcal \vert P(A)\vert=2^{ \vert A \vert}\); \(\mathcal P(A)=\{x\mid x \subseteq A\}\)
Partition	Eine Menge von Teilmengen von A, welche nicht leer sind (\(\bigcup_{i\in I}P_i=A\)) (nicht leer, paarweise disjunkt, Vereinigung gibt Ursprungsmenge)
Kardinalität/Mächtigkeit	Anzahl Elemente in Menge
Schnittmenge (\(X \cap Y\))	Alle Elemente, welche in beiden enthalten sind (\(X\cup U=\{x\mid x \in X \wedge x \in Y\}\)) Distributivgesetz: \(A\cap(B\cup C)=(A\cap B)\cup (A\cap C)\) DeMorgan: \((C\setminus A)\cap(C\setminus B)=C\setminus(A\cup B)\)
Vereinigung (\(X \cup Y\))	Alle Elemente von beiden Mengen (\(X\cup U=\{x\mid x \in X \vee x \in Y\}\))
Komplement (\(X\setminus Y)\)	Alle Elemente aus X, welche nicht in Y vorkommen (\(X \cap \bar Y\))
(nicht paarweise) Disjunkte Mengen	Zwei Mengen teilen keine Elemente
paarwweise Disjunkte Mengen	Alle Mengen teilen keine Elemente
Abzählbare Menge	Wenn eine surjektive Funktion \(F: \N \rightarrow X\) existiert: Abzählbar: \(\N\times\N\) , \(\Z\times\Z\),
Überabzählbare Menge	Wenn es keine surjektive Funktion \(F: \N \rightarrow X\) existiert Überabzählbar: \(\mathcal P(\N)\), \([0;1]\); Die Menge aller unendlichen Binärsequenzen (2. Diagonalargument)

Relationen

Begriff	Erklärung
Injektiv (linkseindeutig)	Wenn zu jedem y höchsten ein x gibt
Surjektiv (rechtstotal)	Wenn es zu jedem y mindestens ein x gibt
Funktion (Relation)	Eine Relation, bei welchem ein x Element nicht zwei y Werte gibt. Von einem Element dürfen also nur maximal ein Pfeil wegzeigen.
Bijektive Funktion	Eine Funktion, welche injektiv und surjktiv ist
Homogene Relation	\(A=B, R\subseteq A\times A\)
Wohldefiniertheit	Eine Funktion, welche eine Äquivalenzrelation als Argument nimmt, ist wohldefiniert, wenn \(xRy \Rightarrow F(x)=F(y)\) bedeutet.
Äquivalenzrelationen	Eine reflexive, symmetrische und transitive Relation, in welcher alle Elemente zu einander eine Beziehung haben
Restklasse	Eine Menge von Elementen in einer Äquivalenzrelation, welche miteinander verbunden
\(x\equiv_5y\)	\((x - y) \text{ ist ein vielfaches von 5}\)
transitiver Abschluss (\(R^+\))	Eine Relation \(R^+\), enhält zusätzlich zu R, alle Relation, damit R transitiv wird
reflexiv-transitiven Abschluss (\(R^*\))	Eine Relation \(R^*\), enhält zusätzlich zu \(R^+\), alle Relationen, damit \(R^+\) reflexiv wird.
DAG	Ein gerichteten zyklenfreien Graphen ist ein Graph, welcher keine zyklen enhält
Dipartir Graph	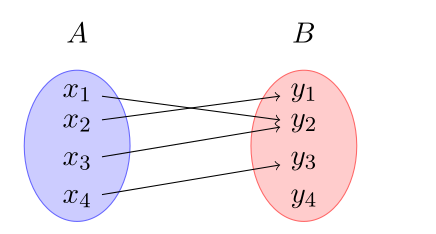Ein Graph, welcher nicht auf einer Homogenen Relation funktioniert
Ordnungsrelation	Ordnung, welche sicherlich reflexiv, transitiv
R-unvergleichbar	Zwei elemente, wenn weder \(xRy\) und \(yRx\) gillt
R-minimal	Ein Element, wenn kein Pfeil auf das Element zeigen
R-maximal	Ein Element, wenn es keine Pfeile weg vom Element zeigen
Präordnung	reflexiv und transitiv
Halbordnung	Eine Präordnung (reflexiv und transitiv), welche auch noch antisymmetrisch ist (zyklenfrei)
totale/lineare Ordnung	Eine Halbordnung (reflexiv, transitiv und antisymmetrisch) ohne R-unvergleichbaren Elemente (zyklenfrei)
Wohlordnung	Eine totale Ordnung, bei welcher alle nicht leeren Teilmenge mindestens ein R-minimales Element (Element, auf welches keine Pfeile zeigen) enhalte (zyklenfrei)
topologische Sortierung	Einen Pfad von Elemente, welche alle miteinander verbunden sind. Matematisch ist dies eine Ordnung: \((\preceq) \subseteq (M\times M\)). \(a\preceq b\) sagt aus, dass a der Vorgänger von b ist

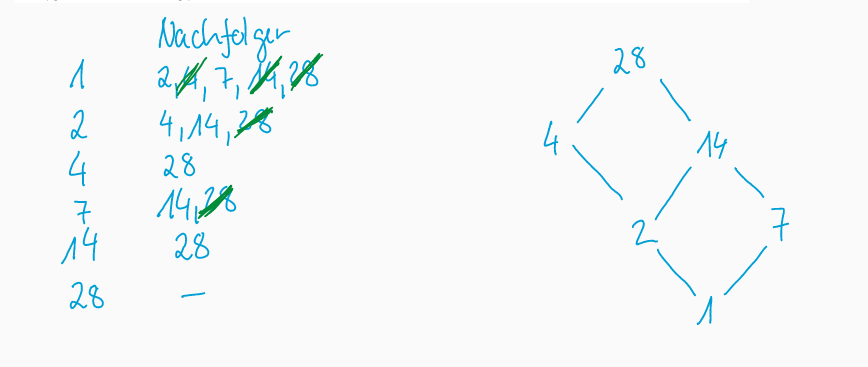
Hase Diagram

Funktioniert nur auf Halbordnungen, welche DAGs sind (also zyklen frei). Für grössere Diagramme kann man alle Elemente mit ihren Nachfolgern aufschreiben und danach alle Nachfolger streichen, welche ein Nachfolger eines Nachfolgers sind. Es lohnt sich zudemmit dem R-maximalen Element zu starten.

Volständige Induktion

1. IV - Induktions Verankerung: \(A(0)\), \(A(1)\), oder anderen Startwert
2. IA - Induktions Annahme: \(A(n)\)
3. IB - Induktions Behauptung: \(A(n+1)\)
4. IS - Induktions Schluss: \(A(n)\Rightarrow A(n+1)\)

Kleinster Verbrecher

Es gibt eine Aussage \(A(n), n\in \N\), welche wahr sein soll.

1. Behauptung: Es gibt ein "kleinsten Verbrecher" aka. die kleinste Zahl, welche die eigentlich Behaupt verletzt. (\(A(n_0):f\))
2. Man versucht nun mit der kleinsten Zahl aus \(\N\), \(0\): \(A(0): t\) \(\Rightarrow\) Daher muss gelten \(n>0 \Rightarrow k+1=n\) (wobei \(k\in \N\))
3. Nun kann \(k+1\) als \(n\) in \(A(n)\) eingesetzt werden (\(A(k+1)\)). Falls dies ein Wiederspruch ergibt, ist die Aussage \(A(n)\) wahr, da es keinen kleinsten Verbrecher gibt

Teilbarkeit

Begriff	Erklärung
\(x\mid y\)	X teilt y (achtung Reihenfolge)
\(T(x)\)	Menge aller Teile von \(x\) (\(T(15)=\{1, 3, 5, 15\}\))
\(\pi(n)\)	Wie viel Primzahlen kleiner als n sind
Prime Restklassen (\(\Z^*_{/7}\))	Eine Menge von Elementen mit einem multiplikativen inversem Element
Faktormenge (\(X_{/R}\))	Die Menge aller Äquivalenzklassen von \(X\) modulo \(R\) \(X_{/R}=\{[x]_R\mid x \in X\}\)
Peano-Axiomen	Die Zahl 0 ist eine natürliche Zahl. Jede natürliche Zahl \(k\) hat gtenau einen Nachfolger \(k+1\), welcher auch eine natürliche Zahl ist. Die Zahl \(0\) ist die einzige Zahl, welc

Rechnenregeln ggT

• \(n\cdot m=kgv(n, m)\cdot ggT(n, m) \Rightarrow kgV(n, m)=\frac{n \cdot m}{ggT(n, m)}\)
• \(ggT(n, n)=n\)
• \(ggT(n, 1)=1\)
• \(ggT(n, 0)=n\)
• \(ggT(n, m)=ggT(n, m-n)\)
• \(ggT(n, m)=ggT(n, m-k\cdot n)\), wenn \(k\cdot n \le m\)
• \(ggT(n, m)=a\cdot n + b \cdot m\), wenn \(x\neq y\) und \(a,b \in \N\)

Um das \(kgV(x, y)\) zu bestimmen, wird eine Primfaktorzerlegung von \(x\) und \(y\) durchgeführt. Danach werden die höchsten Potenzen zusammen gerechnet. Für den \(ggT\) werden die tiefsten Potenzen verwendet.

(Erweiterten) Euklischer Algorithmus

\[ x_0=1\\ x_1=0\\ x_k=x_{k-2}-q_k\cdot x_{k-1}\\ \space \\ y_0=0\\ y_1=1\\ y_k=y_{k-2}-q_k\cdot y_{k-1} \]

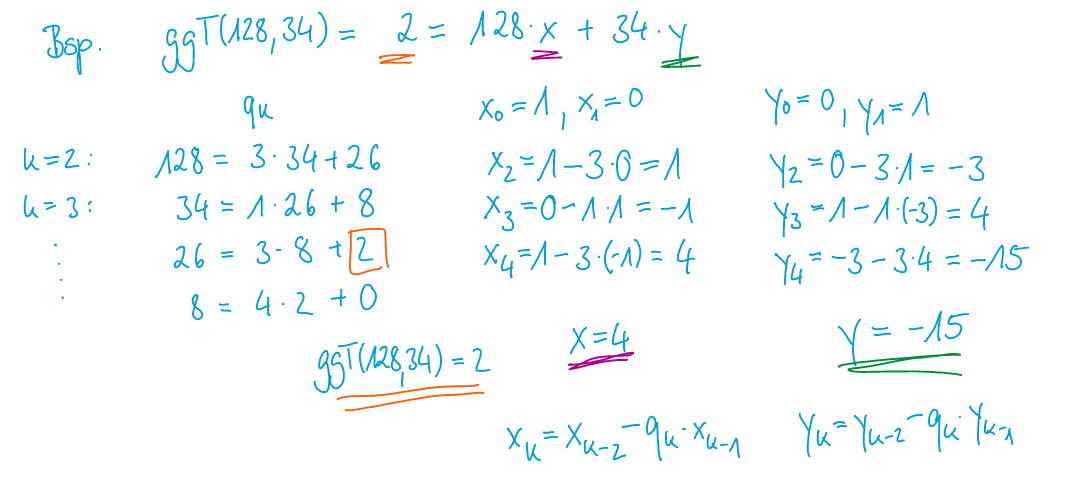
Modulare Arithmethik

für Multiplikation:

• neutrales Element: \([1]_n\)
• inverses Element:
• Nur Zahlen, welche teilefrmed sind (\(ggT(Zahl, N)=1\))
• Eine Zahl multipliziert mt ihrem inversen Element gibt \(1\)
• Kann mit dem Erweiterten Euklidischen Algorithmus berechnet werden: \(Zahlenbereich \cdot x + Zahl \cdot y=1\) \(\Rightarrow y\) ist das multiplikative Inverse. (Zahl muss kleiner sein als Zahlenbereich, sonst muss gewechselt werden)

Eulerische \(\varphi\)-Funktion

Findet die Möchtigkeit einer Prime Restklassen heraus:

1. \(\varphi(n\cdot m)=\varphi(n)\cdot \varphi(m)\), wobei gillt \(ggT(n, m)=1\)
2. \(\varphi(p)=p-1\), wobei gillt \(p\in \mathbb P\)
3. \(\varphi(p^k)=p^k-p^{k-1}\), wobei gillt \(k\in \N_{\gt0}\)

Beispiel:

\[ |\Z_{/8}^*|=\varphi(8)=\varphi(2^3)=2^3-2^{3-1} = 8 -4 =4\\ |\Z_{/15}^*|=\varphi(15)=\varphi(3\cdot5)=\varphi(3)\cdot \varphi(5)\\ |\Z_{/240}^*|=\varphi(240)=\varphi(2^4\cdot3\cdot5)=.. \]

Chinesischer Restsatz

Es gibt garantiert eine Lösung, wenn alle Modulos paarweise teilerfremd sind (alle mit allen den \(ggT\) von \(1\) haben)

Beispiel, um zu sehen, wie \(a_1\) und \(m_1\) zustande kommen: \(\(\begin{aligned} x\equiv_3 2 & \rightarrow &a_1=2 &m_1=3\\ x\equiv_5 7 & \rightarrow &a_2=3 &m_2=5\\ x\equiv_7 2 & \rightarrow &a_3=2 &m_3=7 \end{aligned}\)\)

1. \(M_k\) berechnen: \(M_k=\frac{\prod m_i}{m_k}\)
2. Das multiplaktive Inverse \(N_k\) für jedes \(M_k\) berechnen mit dem Module der Linie k
3. Das Ergebnis mit \(x=\sum^n_{k=1}a_kM_kN_k\) berechnen

\(x\) ist im Modulo \(\prod_{i=1}m_i\) (das Produkt von allen Modulos)

Kleiner Satz von Fermat

Für \((p \in \R \wedge a \in \Z)\wedge p \not{|} a\) gillt \(a^{p-1}\equiv 1 \mod p\)

Beispiel:

\[ \begin{aligned} \begin{gathered} 26^{123}\mod 7 & ggT(26, 7)=1\\ 26^{7-1}\equiv_7 26^6\equiv_7 1\\ 26^{123}\equiv_7 (26^6)^{20}\cdot 26^3\equiv_7 1^20\cdot 26^3\equiv_7 5^3\equiv_7(-2^3) \equiv_7 -8 \equiv_76 \end{gathered} \end{aligned} \]