In dieser Datei werden alle Formeln und Konstanten zusammen gefasst.
| Prefix |
Exponent |
| peta |
\(10^{15}\) |
| tera |
\(10^{12}\) |
| giga |
\(10^9\) |
| mega |
\(10^6\) |
| kilo |
\(10^3\) |
| hecto |
\(10^2\) |
| deca |
\(10^1\) |
| - |
\(10^0\) |
| dezi |
\(10^{-1}\) |
| cento |
\(10^{-2}\) |
| milli |
\(10^{-3}\) |
| micro |
\(10^{-6}\) |
| nano |
\(10^{-9}\) |
| pico |
\(10^{-12}\) |
| femto |
\(10^{-15}\) |
Elektronik
| Thema |
Formeln |
Erklärung |
|
\(I [A]\) |
Strom |
|
\(U [V]\) |
Spannung |
| Wiederstände |
\(U=R\cdot I\) |
Formel für Ohmnische Wiederstände |
| Wiederstände |
\(R_{12}=\frac 1 {\frac 1 {R_1} + \frac 1 {R_2}}\) |
Formel zum zwei parallele Wiederstände zusammen zu fassen |
| Kondensator |
\(CU_c=Q\) |
Der Zusammenhang zwischen der Spannung \(U\) und der Ladung \(Q\) |
| Kondensator |
\(Q(t)=CU_0(1-e^{-\frac t{RC}})\) |
Wie sich die Ladung \(Q\) beim Laden |
| Kondensator |
\(U_C(t)=\frac{Q(t)}{C}=U_0(1-e^{-\frac t{RC}})\) |
Wie sich die Spannung \(U\) beim Laden verhaltet |
| Kondensator |
\(I(t)=\frac{U_0}{R}e^{-\frac t {RC}}\) |
Wie sich der Strom \(I\) beim Laden verhaltet |
| Kondensator |
\(\tau=R\cdot C\) |
Der Kondensator fällt/steigt auf ca \(\frac 1 e\approx0.37\) auf/ab in der Zeit \(\tau\)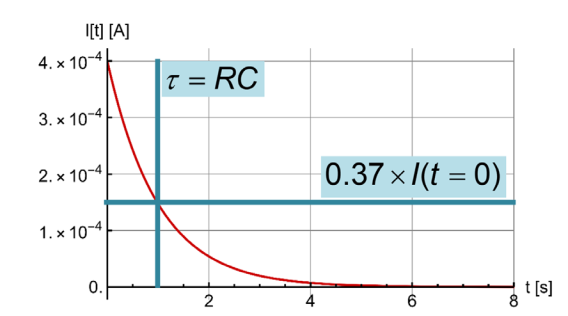 |
Themische Strahlungen
| Konstante |
Erklärung |
| \(c=3\cdot 10^8m/s\) |
Lichtgeschwindigkeit im Vakum |
| \(h=6.626\cdot10^{-34} Js\) |
Planck'sche Konstante |
|
|
| Formel |
Erklärung |
| \(c=\lambda \cdot\nu\) |
Dies ist der Zusammenhang zwischen der Wellenlänge \(\lambda\) und der Frequenz \(\nu\) . \(c\) ist die Lichtgeschwindigkeit |
| \(E=h\nu\) |
Die Energie einer Strahlung mit der Frequenz \(\nu\). \(h\) ist die Plank'sche Konstante |
| \(\rho(\nu)=1-\alpha(\nu)\) |
Umrechnungs Formel zwischen Reflektionskoeffizenten (\(\rho\)) und Absorptionskoeffizenten (\(\alpha\)) |
|
|
|
|
Noch zu lernen
- B-Felder induziert E-Felder
- In welche Richtung positive E-Felder anziehen oder abstossen
