Nullstellen
Fixpunktiteration
Für das benützten der Fixpunktiteration muss die Gleichung in der Fixpunktform \(F(x)=x\) sein. $$ x_{n+1}=F(x_n) $$
Damit die Fixpunktiteration zum Resultat konvergiert, muss für die Ableitung \(F'(x)<1\) gelten. Dies wird auch im Banachscher Fixpunktsatz wiedergespiegelt.
Banachscher Fixpunktsatz
Es gilt folgendes für \(F: [a, b] \to [a, b]\) und die Konstante \(\alpha \in ]0, 1[\) $$ |F(x) - F(y)|\le \alpha\cdot |x - y| \text{ wobei gilt: } x, y\in [a, b]\ \text{oder}\ \frac{|F(x)-F(y)|}{|x - y|} \le \alpha $$ In Deutsch heisst dies, dass die Differenz \(F(x) - F(y)\) nie grösser als \(x-y\) sein darf, oder dass die Steigung nicht grösser als \(1\) darf sein und muss grösser als 0 sein.
Mathematischer: \(F\) muss Lipschitz-stetig (selbst-abbildend) und kontraktiv sein. Zum argumentieren, dass es selbst abbildend ist, \(F(x)\) muss monoton steigend sein (darf nie sinken) und \(F(a)\) und \(F(b)\) müssen zwischen \(a\) und \(b\) sein.
Zum argumentieren, dass es kontraktiv ist, muss \(F(x)\)
Wenn dies gegeben ist,
- hat \(F\) genau einen Fixpunkt \(\overline x\) in \([a, b]\)
- konvergiert die Fixpunktiteration \(x_{n+1}=F(x_n)\) gegen \(\overline x\) für alle Startwerte \(x_0\in [a, b]\)
- Die a-priori und a-posteriori Abschätzungen gelten
\(\alpha\) kann auch als die grösstmögliche Steigung definiert werden: $$ \alpha \in ]0, 1[\ \alpha =\max_{x_0\in[a, b]} |F'(x_0)| $$
Newton-Verfahren
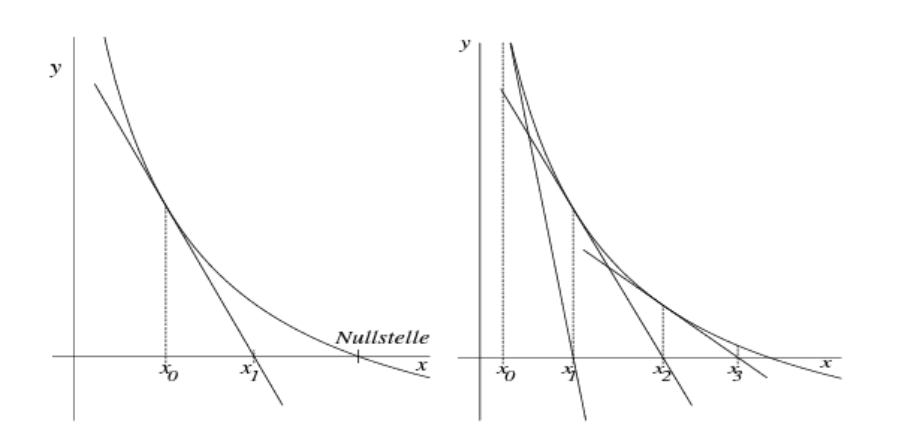$$
x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}
$$
Um sicherzustellen, dass das Newton-Verfahren für einen Startwert \(x_0\) zum Resultat konvergiert, sollte die folgende Bedingung zutreffen:
$$
\left|\frac{f(x) \cdot f''(x)}{[f'(x)]^2}\right|< 1
$$
Diese Bedingung wird typischerweise für den Startwert \(x_0\) überprüft.
Vereinfachtes Newton-Verfahren
Beim vereinfachten Newton-Verfahren wird die Steigung von \(x_0\) für alle Iterationen verwendet: $$ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_0)} $$
Sekanten-Verfahren
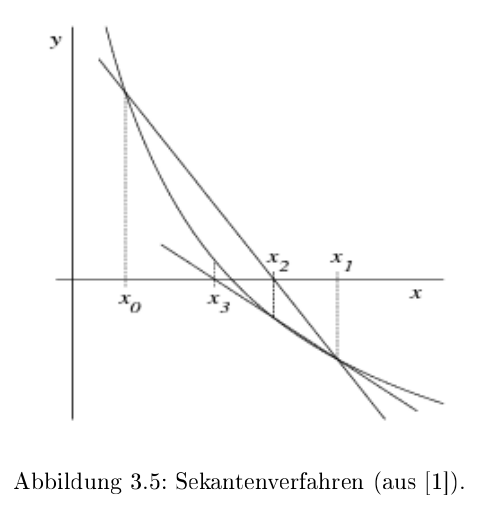$$
x_{n+1}=x_n-\frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}\cdot f(x_n)
$$
Beim Sekanten-Verfahren wird die Ableitung von \(f\) nicht benötigt, da die Steigung mit \(\frac{f(x_1) - f(x_0)}{x_1 - x_0}\) berechnet wird.
Konvergenzordnung
Das \(c \in ]0, \infty[\) ist eine Konstante (wie bei Big-O). \(|x_{n+1}-\overline x|\) ist der absoluten Fehler von \(x_{n+1}\). Wenn \(q=1\) ist, dann konvergiert es linear (meist wird dabei auch noch \(c < 1\) verlangt). Bei \(q=2\), quadratisch, und so weiter.
Fehlerabschätzung
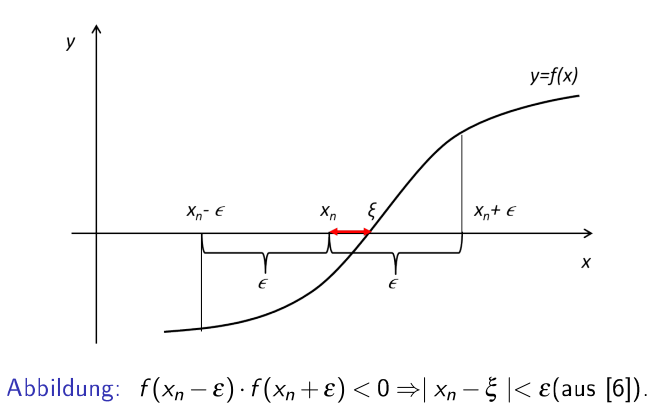
\(x_n\) ist eine mit iterieren erreichte Nullstelle, \(\varepsilon\) ist ein maximalen Fehler, welcher Verlangt ist und \(\overline x\) ist die exakte Nullstelle. $$ f(x_n+\varepsilon)\cdot f(x_n-\varepsilon)<0 \Rightarrow \vert x_n - \overline x\vert < \varepsilon $$ Oder auf Deutsch: Wenn es einen Vorzeichenwechsel zwischen \([x_n-\varepsilon; x_n + \varepsilon]\) gibt, dann gibt es eine Nullstelle \(\overline x\) in diesem Intervall. Aus dem ergibt sich, dass die Differenz zwischen der Nullstelle \(\overline x\) und \(x_n\) muss kleiner als \(\varepsilon\) sein
a-priori und a-posteriori Abschätzung
Mit der a-priori Abschätzung kann der maximale absolute Fehler nach \(n\) Iterationen von den ersten zwei Iterationen \(x_0\) und \(x_1\) geschätzt werden: $$ |x_n-\overline x|\le \frac{\alpha^n}{1-\alpha}\cdot |x_1 - x_0|\ n=\log_\alpha\left ( \frac{|x_n - \overline x|\cdot (1-\alpha)}{|x_1 - x_0|}\right ) $$ Mit der a-posteriori Abschätzung kann der maximale absoluten Fehler nach \(n\) Iterationen von der \(n\)-ten und \(n-1\)-te Iteration abschätzen: $$ |x_n-\overline x|\le \frac \alpha {1- \alpha}\cdot|x_n - x_{n-1}| $$