Komplexitätstheorie
Es gibt mehrere Arten von Komplexität:
- Zeitkomplexität: Laufzeit des besten Programms, welche ein Problem löst
- Platzkomplexität: Speicherbedarf des bestens Programmes
- Beschreibungskomplexität: Länge des kürzesten Programmes


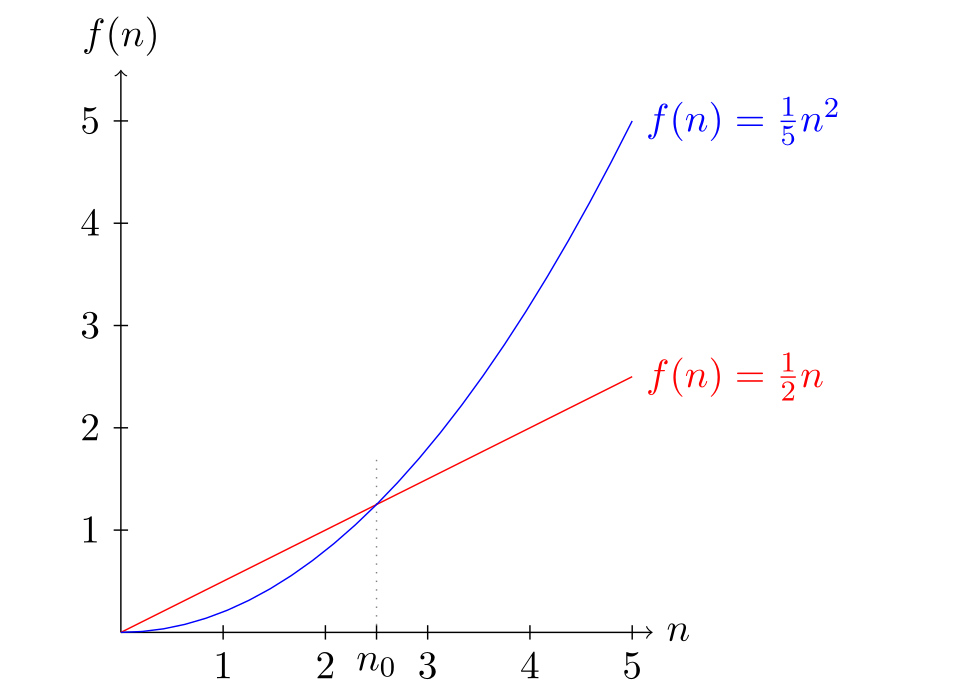
Big-O-Notation (Landau Symbol)


Im folgende Beispiel gilt:
- \(7n+4\in \mathcal O(n)\) für \(n \ge 6 = n_0\)
- \(0.5n^2+5n - 4 \in \mathcal O(n^2)\)
Bespiel an Turing Maschinen
Klassifizierung von Problemen (NP vs P)



Polynomzeit Verifizieren
Ein Polynomzeit-Verifizierer ist eine Turing-Maschine, welche in polynomen Zeit (\(\mathcal O(n^k)\), wobei gilt \(k \in \N\)) überprüft, ob das Resultat einer Berechnung stimmt.
**Frage: ** Sind p-Verifizierer und Polynomzeit-Verifizierer das selbe? --> Ja
Alle Probleme, welche ein Polynomzeit-Verifizierer haben, sind in der Gruppe \(NP\) enthalten.


Polynomielle Reduktion
Eine Sprache \(L_1\) ist polynominell auf \(L_2\) reduzierbar (\(L_1 \preceq_p L_2\)), wenn eine Turing Maschine gebaut werden kann, welche von \(L_1\) zu \(L_2\) umwandeln kann. Dies muss in \(O(n^k)\) möglich sein.
NP-Schwer und NP-Vollständig
Ein Problem ist NP-schwer, wenn es auf alle NP-Probleme (Probleme, welche mit einer Nicht-Deterministiersch-Maschine lösbar/verifizierbar sind) reduzieren lässt. Aus dem geht hervor, dass ein Problem, welches NP-schwer ist, gleich schwer oder schwerer zum lösen ist, wie alle NP-Problem einzeln.
Ein Problem ist NP-vollständig, wenn es ein NP-Problem und NP-schwer ist.
Ein NP-vollständiges Problem ist gleich schwer zum lösen, wie das am schwierigsten lösbaren NP-Problem.
\(P=NP\) Problem
Wenn es jemandem gelingt ein Problem zu finden, welches NP-vollständig ist und gleichzeitig auch zu P gehöhrt, dann würde gelten \(P=NP\), da P zu jedem NP-Problem reduziert werden könnte.
Bis jetzt wurde kein solches Beispiel gefunden
Konjunktive Normalform (KNF)
Ein Ausdruck, welcher in der konjuktiver Normalform steht, besteht nur aus \(\neg\), \(\vee\), \(\wedge\), \(()\) und Literale.
Beispiele:
- \(x\)
- \(x_1 \vee x_2\)
- \(x_1 \wedge x_2\)
- \((x_1 \vee x_2) \wedge (x_3 \vee x_4) \wedge \neg x_5\)
Hingegen \((x_1 \wedge x_2) \vee x_3\) wäre nicht in der konjunktive Normalform
SAT
SAT war das "erste" NP-vollständige Problem. Anhand diesem wurden alle weiteren Beweise für NP-Vollständigkeit aufgehängt.
Das SAT Problem ist zu einscheiden, ob eine Formel in der KNF erfüllbar ist. Also es sicherlich eine Belegung gibt, welche 1 zurück gibt.
Es muss gezeigt werden das:
- \(SAT \in NP\): Es ist möglich eine Nicht-Deterministische Maschine zu bauen, welche überprüfen kann, ob eine Formel erfüllbar ist
- SAT ist NP-schwer: Das Problem kann zu allen NP-Problemen reduziert werden
NP-Vollständigkeits-Nachweis weiteren Problemen
Satz Wenn \(P1\) NP-schwer und \(P2\) in NP enthalten ist und eine polynomielle Reduktion \(P1 \preceq_p P2\) existiert, dann ist \(P2\) NP-vollständig.
Dass heisst, wenn ein Problem in NP enthalten ist und es eine Reduktion zu dem SAT Problem gibt, dann ist es NP-vollständig.
