Impuls
Der Impuls ist definiert als: $$ \vec p = m \vec v $$ (Dabei ist \(m\) eine Masse in kg und \(\vec v\) eine Geschwindigkeit)
Der Gesamtimpuls eines Systems bleibt immer erhalten, insofern keine äusseren Kräfte einwirken.
Stossexperiment

| \(m_1\) | \(\Delta v_1\) | \(m_2\) | \(\Delta v_2\) | \(\frac{m_1}{m_2}\) | \(\frac{\Delta v_2}{\Delta v_1}\) |
|---|---|---|---|---|---|
| \(0.5\) | \(-1\) | \(0.5\) | \(+1\) | \(1\) | \(-1\) |
| \(0.25\) | \(-11.5\) | \(0.5\) | \(+5.5\) | \(0.5\) | \(-0.5\) |
Aus diesem Experimentt geht, dass folgendes gilt: $$ \begin{align} \frac{m_1}{m_2}&=-\frac{\Delta v_2}{\Delta v_1}\ m_1 \cdot \Delta V_1 &= -m_2 \cdot \Delta v_2 \end{align} $$ Oder in Worten: den Impuls bleibt erhalten. Körper 1 gibt den Impuls weiter an den Körper 2.
Elastischer Stossversuch
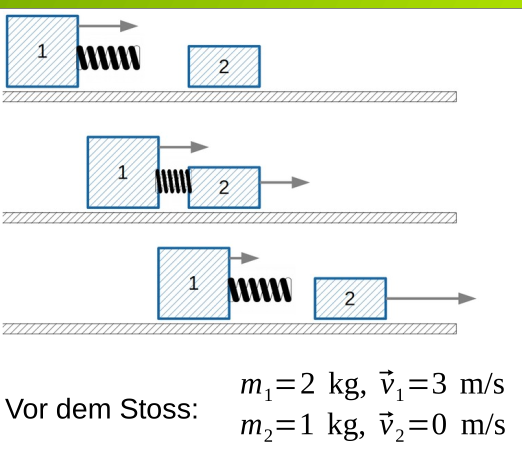
Der Gesamtimpuls des gesamten Systems ist \(V_{Spt}=\frac{m_1 \vec v_2 + m_2 + }{}\)
Aus diem geht er TODO $$ \vec p_{vor}=\vec p_1+\vec p_2=m_1 \cdot \vec v_1 + m_2 \cdot \vec v_2 = 6 \frac{kg\cdot m}{s} = \vec p_{nach} \ $$
Unelastischer Stossversuch


Der Gesamtimpuls ist
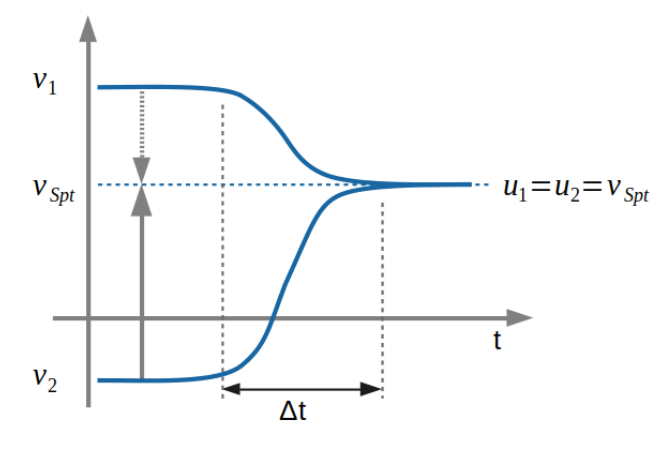
$$ \begin{align} \vec p_{vor}&=m_1\vec v_1 + m_2 \vec v_2 = \vec p_{nach} = (m_1 + m_2) \cdot \vec u\ \vec u &=\frac{m_1\vec v_1 + m_2 \vec v_2}{m_1 + m_2} \end{align} $$ In einem Zeit-Geschwindigkeits-Diagramm sieht das folgendermassen aus:
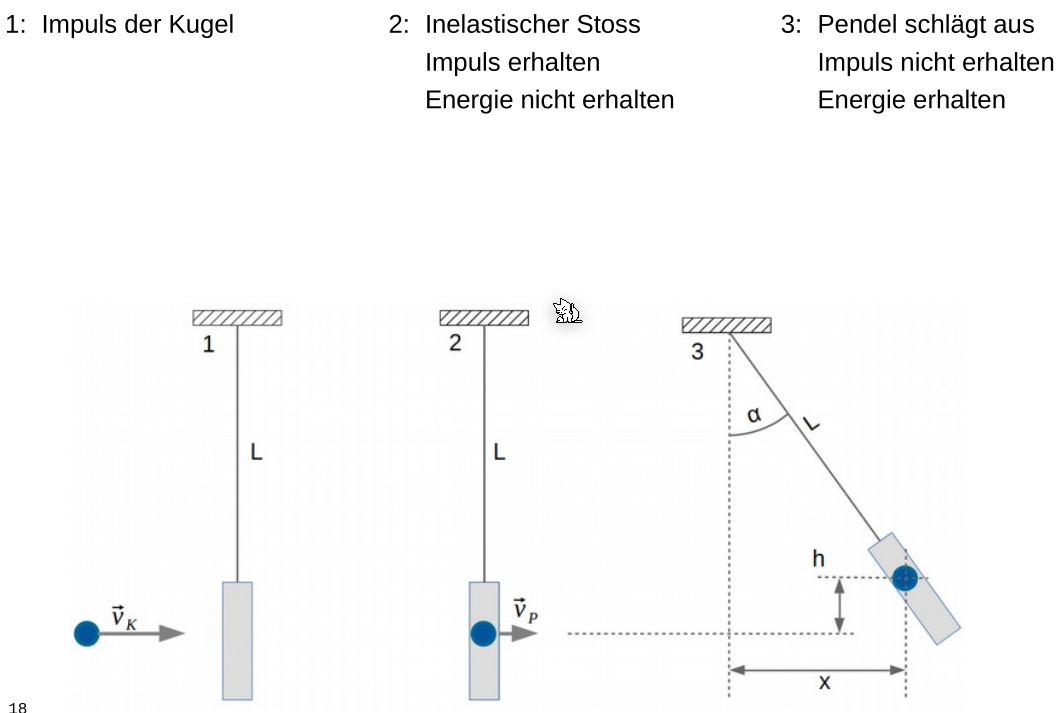
Ballistisches Pendel
https://www.leifiphysik.de/mechanik/impulserhaltung-und-stoesse/versuche/ballistisches-pendel-simulation

Schwerpunkt Geschwindigkeit
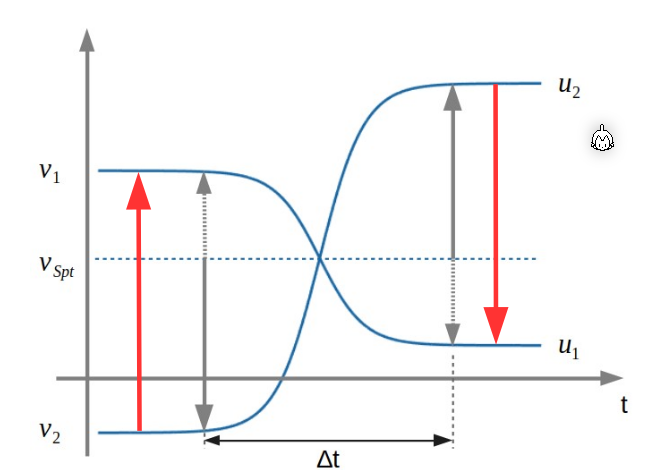
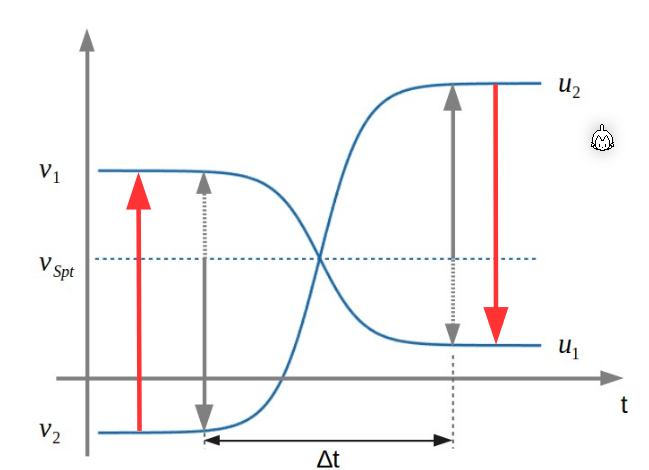
\(V_{Spt}\) ist die Schwerpunkt Geschwindigkeit und stellt die Spiegelachse dar, an dem sich die Geschwindigkeitsidifferenzen spiegeln. $$ V_{Spt}=\frac{\vec p}{m_1+m_2}=\frac{m_1\cdot \vec v_1 + m_2 \cdot \vec v_2}{m_1+m_2} $$ Im Falle der Elastischen Stosses, wird das \(u_1\) und \(u_2\) nach dem Zusammenstoss an \(V_{Spt}\) gespiegelt.
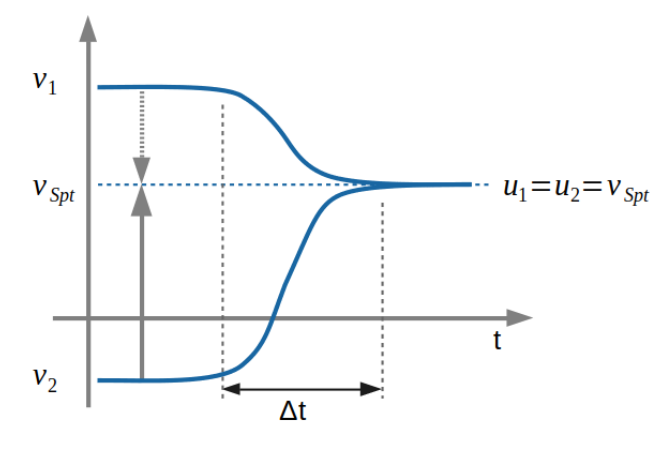
Im Falle des unelastischen Stosses gilt nach dem Stoss \(u_1=u_2=v_{Spt}\)
Wenn gillt \(m_2 \gg m_1\), dann gelten folgende vereinfachten Formeln: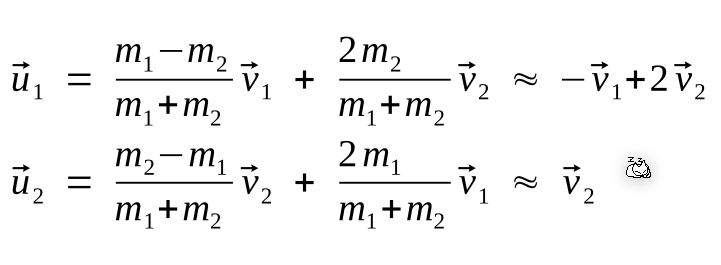
Kraftstoss
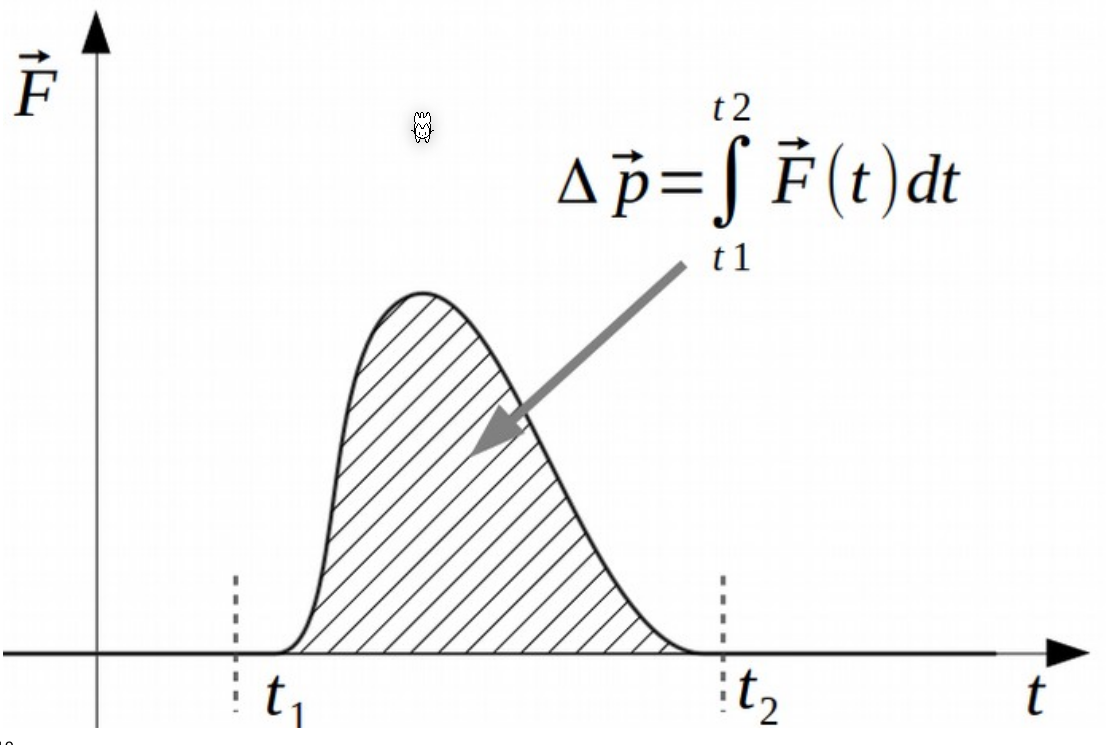
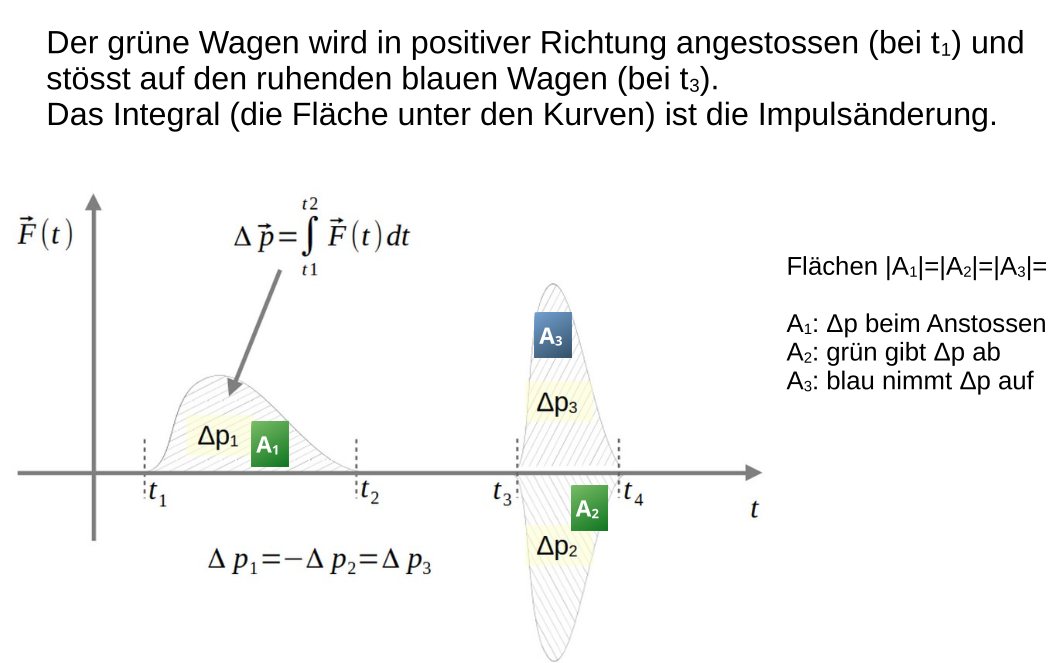
Die Impulsänderung durch einen Kraftstoss ist die Fläche einer \(F(t)\) Funktion.
Im folgenden Diagramm ist grafisch dargestellt, wie der Impuls erhalten bleibt.
Racketen
\(v_{final}\) ist die finale Geschwindigkeit, \(v_{Gasse}\) ist die Austrittsgeschwindigkeit der Gasse, \(m_{init}\) ist die initiale Masse und \(m_{final}\) ist die finale Masse (ohne Treibstoff).