Entschheidbarkeit

Eine Sprache \(A \subset \Sigma^*\) heisst entscheidbar,, wenn eine Turingmaschine \(T\) existiert, die das Entscheidungsproblem \((\Sigma, A)\) löst (Dabei ist \(A\) die Menge aller akzeptierter Zustände).

Wenn der Bandinhalt \(x \in A\) ist, hält \(T\) nach endlichen vielen Schritten mit dem Bandinhalt 1 and, wenn der Bandinhalt \(x \in \overline A\) ist, dann hält \(T\) nach endlichen vielen Schritten mit dem Bandinhalt 0 an. Wichtig: Egal was für ein Input auf dem Band steht, \(T\) muss immer anhalten.

Oder anders ausgedrückt, es müssen alle akzeptierte Inputs \(A\), wie auch alle nicht akzeptiert Inputs \(\overline A\) semi-entscheidbar sein.

Eine Sprache wird Semi-Entsheidbarkeit genannt, wenn es eine Turingmachine \(T\) gibt, welche bei dem Bandinhalt \(x \in A\) (\(A\) ist die Menge der akzeptierten Inputs) in endlichen vielen Schritten mit dem Bandinhalt 1 für Ja endet. Wenn der Bandihalt \(x \in \Sigma^*\setminus A\) (als x nicht ein akzeptierter Zustand ist), hält die Turingmachine \(T\) nie an.

Für jede entscheidbare Sprache kann eine Turningmaschine geschrieben werden, welche semi-entscheidbar ist.

\(\cup\) und \(\cap\) Satz

Wenn \(A\) und \(B\) entscheidbar ist, dann ist auch \(A\cup B\) und \(A\cap B\) entscheidbar. Wenn \(A\) und \(B\) semi-entscheidbar ist, dann ist auch \(A \cup B\) und \(A\cap B\) semi-entscheidbar.

Reduktion

Sätze

• Transitivität: Für beliebige Sprachen \(A, B\) und \(C\) und \(A \preceq B\) und \(B \preceq C\) gilt, dann gilt auch \(A \preceq C\)

• Für beliebige Sprachen \(A\) und \(B\), wenn \(B\) entscheidbar ist und \(A \preceq B\) gilt, dann ist auch \(A\) entscheidbar.

• Für beliebige Sprachen \(A\) und \(B\), wenn \(B\) semi-entscheidbar ist und \(A \preceq B\) gilt, dann ist auch \(A\) semi-entscheidbar.

Allgemeine Halteproblem

Leeres-Band Halteproblem

Spezielle Halteproblem

Halteproblem Beweiss

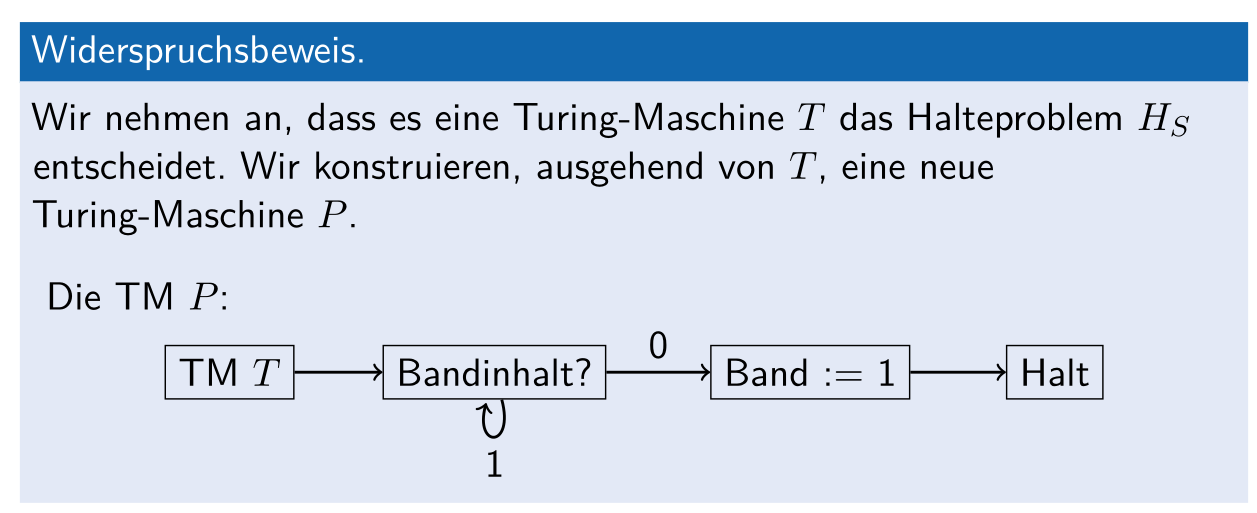
Satz von Rice

Es gibt eine Menge \(R\), in welcher alle berechenbare Funktion sind. Die Menge \(S\subset R\) ist eine echte, nicht leere Teilmenge von R. Die folgende Sprache ist nun unentscheidbar: $$ C(S)={w\in{0,1}^*\mid F_w\in S} $$