Spezielle Verteilung
Normalverteilung
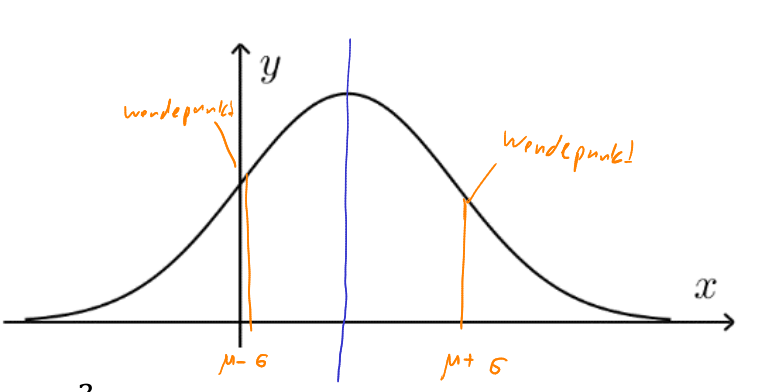 $$
\varphi_{\mu, \sigma}(x)=\frac {1}{\sqrt{2\pi}\cdot \sigma}\cdot e^{-\frac 1 2((x-\mu) : \sigma)^2}\
$$
$$
\varphi_{\mu, \sigma}(x)=\frac {1}{\sqrt{2\pi}\cdot \sigma}\cdot e^{-\frac 1 2((x-\mu) : \sigma)^2}\
$$
- Die Normalverteilung ist normiert, heisst dass \(\int^\infty_{-\infty}\varphi(x)dx=1\) Daher, je grässer \(\sigma\) wird, desto breiter und niedriger wird die Glockenkurve.
Zentraler Grenzwert
Wenn eine Liste von identische verteilte und stochastisch unabhängige Zufallsvariablen \(X_1, X_2, ..., X_n\) haben, dann