Nichtlineare Gleichungssysteme

Multivariate Funktionen

Skalarwertige Funktion

Eine Funktion, welche mehrere $x$-Werte nimmt und ein $y$-Wert zurück gibt. $$ f: \mathbb R ^n \to \mathbb R \ y = f(x_1, x_2, ..., x_n) $$

Vektorwertige Funktion

Eine Funktion, welche mehrere $x$-Werte nimmt und mehrere $y$-Werte zurück gegeben $$ f: \mathbb R^n \to \mathbb R^m \ (y_1, y_2, ..., y_m) = f(x_1, x_2, ..., x_n) $$

Explizite und implizite Funktionen

Explizite Funktionen haben die folgende Form: $y=f(x_1, x_2, ..., x_n)$

Implizite Funktionen haben die folgende Form: $F(x_1, x_2, ..., x_n, y)=0$

Partielle Ableitung

Um die Funktion $z=f(x, y) = 2x^2 + 5 y$ abzuleiten, kann nach $x$ und $y$ separat abgeleitet werden: $$ \begin{align} \text{nach }x: \frac{\partial f}{\partial x} &= 4x + 0 \ \text{nach }y: \frac{\partial f}{\partial y} &= 0 + 5 \ \end{align} $$ Diese Ableitung kann folgendermassen visualisiert werden:

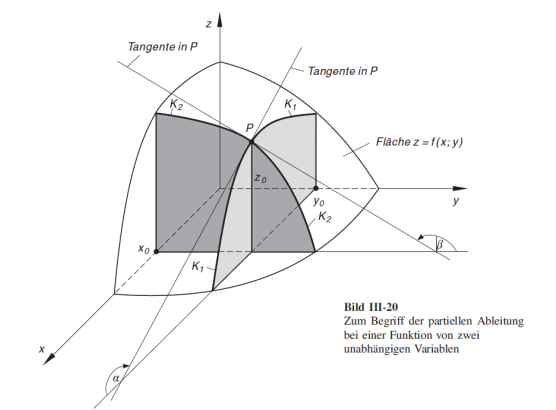
Jacobi-Matrix

Für die Funktion $f: \mathbb R^n \to \mathbb R^m$ mit $\vec y = f(\vec x)=\begin{pmatrix}y_1=f_1(\vec x) \\ y_2 = f_2(\vec x)\\ ... \\ y_m=f_m(\vec x)\end{pmatrix}$ und $\vec x = (x_1, x_2, ..., x_n)^T$ ist die Jacobi-Matrix das folgende: $$ Df(x)=\begin{pmatrix} \frac{\partial f_1}{\partial x_1}(\vec x) & \frac{\partial f_1}{\partial x_2}(\vec x) & ... & \frac{\partial f_1}{\partial x_n}(\vec x) \

\frac{\partial f_2}{\partial x_1}(\vec x) & \frac{\partial f_2}{\partial x_2}(\vec x) & ... & \frac{\partial f_2}{\partial x_n}(\vec x) \

... & ... & ... & ... \ \frac{\partial f_m}{\partial x_1}(\vec x) & \frac{\partial f_m}{\partial x_2}(\vec x) & ... & \frac{\partial f_m}{\partial x_n}(\vec x) \ \end{pmatrix} $$ In dieser Matrix ist in einer Reihe alle möglichen partiellen Ableitungen für $f_1(\vec x)$

Linearisierung

Eine Approximation für $y=f(x)$ kann mit $f(x)\approx f(x_0) + f'(x-x_0)$.

Dasselbe kann auch für eine multivariante Funktion mithilfe der Jacobi-Matrix getan werden: $g(\vec x)=f(\vec {x_0}) + Df(\vec {x_0})\cdot (\vec x-\vec {x_0})$

($Df(\vec x)$ ist die Jacobi-Matrix)

Nach dem Linearisieren wird ein nichtlineare Funktion lineare und kann mit bekannten Verfahren gelöst werde

Newton-Verfahre

Das Newton-Verfahren erwartet, dass $f(\vec x_n)=\vec 0$ gilt.

\[ \vec x_{n+1}=\vec x_n-(Df(\vec x_n))^{-1}\cdot f(\vec x_n) \]

Um nicht die Jacobi-Matrix invertieren zu müssen, kann folgender Trick angewendet werden: $$ \vec \delta_n :=-(Df(\vec x_n))^{-1}\cdot f(\vec x_n)\ \text{Dies kann in folgendes Umgewandlet werden:}\ Df(\vec x_n)\cdot \vec\delta x_n = -f(\vec x_n) $$ Die Gleichung $Df(\vec x_n)\cdot \vec\delta x_n = -f(\vec x_n)$ ist ein lineares Gleichungssystem, welches relativ einfach gelöst werden kann. Danach kann $\vec \delta _n$ anstelle von $-(Df(\vec x_n))^{-1}\cdot f(\vec x_n)$ verwendet werden: $\vec x_{n+1}=\vec x_n+\vec \delta_n$

Das Newton-Verfahren konvergiert quadratisch für nah genug an einer Nullstelle $\overline x$ liegende Startwerte, wenn $Df(\overline x)$ regulär und $f$ dreimal stetig differenzierbar ist.

Für eine Nichtreguläre Matrix A gilt $\det(A)\ne 0$

Mögliche Abbruchskriterien sind:

$n > n_{max}$
$||\vec x_{n+1}-\vec x_n||\le ||\vec x_{n+1}||\cdot \varepsilon$
$||\vec x_{n+1}-\vec x_n||\le \varepsilon$
$||f(\vec x_{n+1})||\le \varepsilon$$

Vereinfachtes Newton-Verfahren

Beim regulären Newton-Verfahren muss bei jeden Iterationsschritt die Jacobi-Matrix $Df(\vec x)$ neuberechnen. Beim vereinfachten Newton-Verfahren wird $Df(\vec x)$ nur für den Startvektor berechnet. $$ \vec x_{n+1}=\vec x_n-(Df(\vec x_0))^{-1}\cdot f(\vec x_n)\ Df(\vec x_0)\cdot \vec\delta x_n = -f(\vec x_n) $$ Wegen dieser Vereinfachung kovergiert das Verfahren nur noch linear gegen die Nullstelle, wenn $Df(\overline x)$ nicht regulär ist.

Gedämptes Newton-Verfahren

Wenn $Df(\vec x_n)$ schlecht konvergiert, dann kann nicht generell erwartet werden, dass $\vec x_{n+1}=\vec x_n + \vec \delta_n$ nicht gilt.

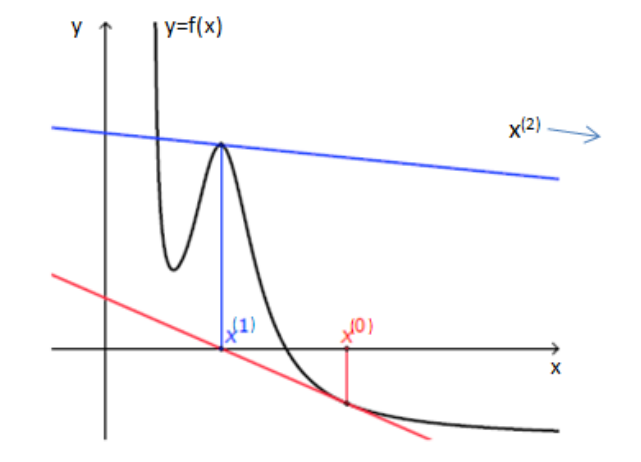
Für das gedämpfte Newton-Verfahren werden folgende Schritte angewendet:

Berechne $\delta_n$ mit $Df(\vec x_n)\delta_n=-f(\vec x_n)$ ausgerechnet
Finde das minimale $k\in \{0, 1, ...\}$ für das gilt: $||f(\vec x_n + \frac{\vec \delta_n}{2^k})||_2 < ||f(\vec x_n)||_2$
Wenn kein $k$ gefunden wird, soll mit $k=0$ weiter gerechnet werden
Nun soll die Iterationsgleichung $\vec x_{n+1}=\vec x_n + \frac{\vec \delta_n}{2^k}$ verwendet werden